Cho hình nón đỉnh S, bán kính đường tròn đáy là R, chiều cao SH= R 3 (cm).
b) Giả sử AB = R 3 là một dây cung của đáy. Tính diện tích tam giác SAB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho hình nón đỉnh S, bán kính đường tròn đáy là R, chiều cao SH= R 3 (cm).
a) Tính thể tích hình nón.

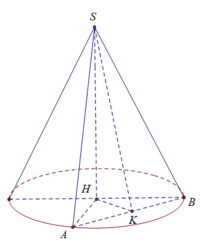
a) SH = R 3 là chiều cao của hình nón
Thể tích của hình nón là:
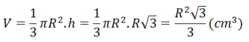

Chọn đáp án A.
Góc ở đỉnh hình nón là φ = 120 ° là góc tạo bởi khi mặt phẳng đi qua trục SO => O S C ^ = 60 °
Khi cắt hình nón bởi mặt phẳng qua đỉnh S tạo thành tam giác đều SAB nên mặt phẳng không chứa trục của hình nón.
Xét tam giác vuông SOC tại O:
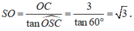
Xét tam giác vuông SOA tại O:
![]()
Do tam giác SAB đều:
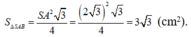
b) Gọi K là trung điểm AB
Do ΔHAB cân tại H (HA = HB = R) nên HK ⊥ AB
Tam giác HAK vuông tại K có: HA = R; KA = (R 3 )/2
Mặt khác ta có: ΔSHK vuông tại H
ΔSAB cân tại S có SK là trung tuyến nên SK cũng là đường cao