Trong mặt phẳng với hệ trục tọa độ Oxy, phép đối xứng qua trục Ox biến điểm thành điểm nào dưới đây?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

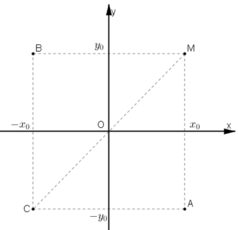
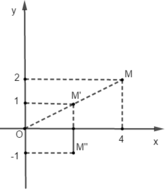
Biểu diễn các điểm trên hệ trục tọa độ ta thấy:
a) Điểm đối xứng với M(x0; y0) qua trục Ox là A(x0 ; –y0)
b) Điểm đối xứng với M(x0 ; y0) qua trục Oy là B(–x0 ; y0)
c) Điểm đối xứng với M(x0 ; y0) qua gốc O là C(–x0 ; –y0).

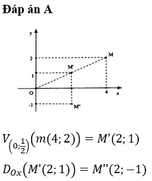
V ( 0 ; 1 / 2 ) ( M ( 4 ; 2 ) ) = M ' ( 2 ; 1 ) ; Đ O x ( M ' ( 2 ; 1 ) ) = M " ( 2 ; - 1 ) .
Đáp án A.

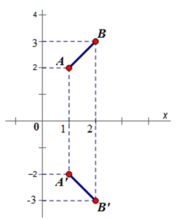
Lấy ảnh A',B' của hai điểm A(1; 2) và B(2; 3) qua phép đối xứng trục Ox
Dùng biểu thức tọa độ của phép đối xứng qua trục Ox, ta có:
A'(1;-2), B'(2;-3)
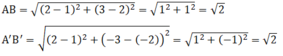
⇒ A'B' = AB

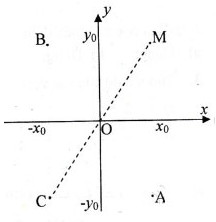
a) Hai điểm đối xứng nhau qua trục hoành thì có hoành độ bằng nhau và tung độ đối nhau.
M0 (x0; y0)=> A(x0;-y0)
b) Hai điểm đối xứng với nhau qua trục tung thì có tung độ bằng nhau còn hoành độ thì đối nhau.
M0 (x0; y0) => B(-x0;y0)
c) Hai điểm đối xứng nhau qua gốc O thì các tọa độ tương ứng đối nhau.
M0 (x0; y0) => C(-x0;-y0)
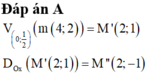
Đáp án D.
Phép đối xứng qua trục Ox biến điểm M a ; b thành điểm M ' a ; − b .
Phân tích phương án nhiễu:
Phương án A: HS nhầm lần với phép đối xứng qua tâm O.
Phương án B: HS nhầm lẫn với phép quay tâm O với góc quay 360°.
Phương án C: HS nhầm lần với phép đối xứng qua trục Oy.