Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Theo tính chất tích phân ta có:
+ ) ∫ a b f ( x ) d x + ∫ b c f ( x ) d x + ∫ c a f ( x ) d x
∫ c a f ( x ) d x + ∫ c a f ( x ) d x = ∫ a a f ( x ) d x = 0
Đáp án A đúng.
+ ) ∫ a b c f ( x ) d x = c ∫ a b f ( x ) d x
với
c
∈
ℝ
.Đáp án B đúng.
+ ) ∫ a b ( f ( x ) - g ( x ) ) d x + ∫ a b g ( x )
= ∫ b a f ( x ) d x - ∫ a b g ( x ) d x + ∫ a b g ( x ) d x = ∫ a b f ( x ) d x
Đáp án D đúng.
Đáp án C sai.
Chọn đáp án C.
Phương pháp: Sử dụng phương pháp đổi biến, đặt t = u(x)
Cách giải:
Đặt
Đổi cận 
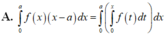
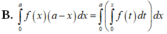
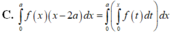
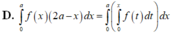
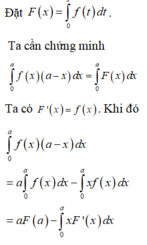
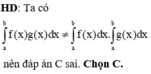
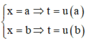
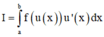
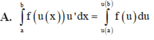
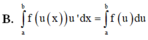
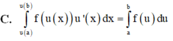
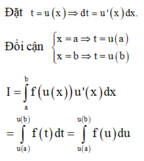
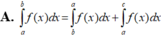
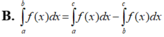
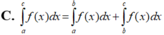
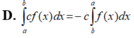
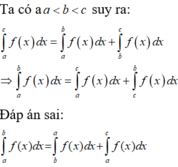
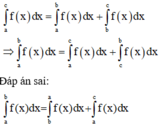
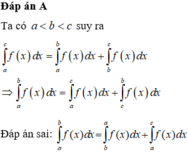
Đặt F x = ∫ 0 x f t d t . Ta cần chứng minh ∫ 0 a f x x - a d x = ∫ 0 a F x d x
Ta có F'(x) = f(x). Khi đó
∫ 0 a f x a - x d x = a ∫ 0 a f x d x - ∫ 0 a x f x d x = a F a - ∫ 0 a x F ' x d x
Sử dụng công thức tích phân từng phần, ta có ∫ 0 a x F ' x d x = a F a - ∫ 0 a F x d x
Thay vào ta thu được kết quả ở B
Đáp án B