Ba người thợ săn cùng bắn vào 1 con thú với khả năng bắn trúng tương ứng là 0,4; 0,5 và 0,7. Tính
a) Xác suất để con thú bị trúng ít nhất 1 viên đạn
b) Biết rằng con thú bị trúng ít nhất 1 viên đạn, tính xác suất để người thợ săn thứ 2 bắn trúng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
3 tháng 12 2019
Ta có : \(\overline{A}=\overline{A_1UA_2UA_3}=\overline{A_1}\) \(\overline{A_2}\)\(\overline{A_3}\)= sự kiện không có ai bắn trúng
\(\Rightarrow P\left(\overline{A}\right)=\)\((\overline{A_1}\)\(\overline{A_2}\)\(\overline{A_3})\)\(=P\left(\overline{A_1}\right)P\left(\overline{A_2}\right)P\left(\overline{A_3}\right)=0,5.0,4.0,3=0,06\)
\(\Rightarrow P\left(A\right)=1-P\left(\overline{A}\right)=1-0,06=0,94\)
Vậy xác xuất để con thú bị bắn trúng là 0,94
CM
10 tháng 4 2018
Chọn A.
Phương pháp:
Áp dụng quy tắc cộng và nhân xác suất.
Cách giải:
Xác suất để có ít nhất một người bắn trúng là:
1 − 1 − 0 , 7 1 − 0 , 6 1 − 0 , 5 = 1 − 0 , 3.0 , 4.0 , 5 = 0 , 94
CM
25 tháng 4 2019
Đáp án C
Gọi X ¯ là biến cố
Không một xạ thủ nào bắn trúng
Do A, B, C độc lập với nhau nên A ¯ ; B ¯ ; C ¯ độc lập với nhau
Suy ra P ( X ¯ ) = 0 , 3 . 0 , 4 . 0 , 5 = 0 , 06
CM
27 tháng 4 2018
Đáp án C
Gọi X ¯ là biến cố: Không một xạ thủ nào bắn trúng. Khi đó X ¯ = A ¯ ∪ B ¯ ∪ C ¯ . Do A, B, C độc lập với nhau nên A ¯ ; B ¯ ; C ¯ độc lập với nhau.
Suy ra P X ¯ = 0 , 3 . 0 , 4 . 0 , 5 = 0 , 06 ⇒ P X ¯ = 1 - P X ¯ = 0 , 94 .
CM
16 tháng 1 2019
Gọi Ai là biến cố:” bắn viên đạn thứ i trúng mục tiêu”i=1,2,3
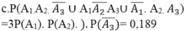
Chọn B
CM
14 tháng 1 2018
Gọi Ai là biến cố:” bắn viên đạn thứ i trúng mục tiêu”i=1,2,3
Chọn A
CM
16 tháng 6 2017
Gọi Ai là biến cố:” bắn viên đạn thứ i trúng mục tiêu”i=1,2,3
Chọn C
AH
Akai Haruma
Giáo viên
12 tháng 1 2023
Lời giải:
a. Xác suất chỉ người thứ nhất bắn trúng là:
$0,1(1-0,2)(1-0,3)=0,056$
b. Xác suất không người nào bắn trúng: $(1-0,1)(1-0,2)(1-0,3)=0,504$
Xác suất có ít nhất 1 người bắn trúng: $1-0,504=0,496$
c. Xác suất cả 3 người bắn trúng: $0,1.0,2.0,3=0,006$
d.
Xác suất người đầu bắn trúng và người 2 trượt:
$0,1(1-0,2)=0,08$
e.
Xác suất có đúng 1 người bắn trúng:
$0,1(1-0,2)(1-0,3)+(1-0,1).0,2.(1-0,3)+(1-0,1)(1-0,2)0,3=0,398$
f. Xác suất có ít nhất 2 người bắn trúng:
1- xác suất cả 3 cùng trượt - xác suất chỉ có 1 người bắn trúng
= $1-(1-0,1)(1-0,2)(1-0,3)-0,398=0,098$
g.
Xác suất không có quá 2 người bắn trúng
= 1- xác suất cả 3 người trúng = $1-0,1.0,2.0,3=0,994$