(GIÚP MÌNH CÂU C)
Cho góc xOy=60o. Lấy A nằm bên trong góc xOy. Gọi B đối xứng với A qua Ox. C đối xứng với A qua Oy.
a) So sánh OB và OC
b) Tính góc BOC.
c)Qua B vẽ tia BZ//OA; BZ cắt Ox tại E. Chứng minh AOBE là hình bình hành
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 11 2021
a: Ta có: A và B đối xứng nhau qua Ox
nên OA=OB(1)
Ta có: A và C đối xứng nhau qua Oy
nên OA=OC(2)
Từ (1) và (2) suy ra OB=OC
24 tháng 8 2023
a: A đối xứng B qua ox
=>OA=OB
=>ΔOAB cân tại O
=>Ox là phân giác của góc AOB(1)
A đối xứng C qua Oy
=>OA=OC
=>ΔOAC cân tại O
=>Oy là phân giác của góc AOC(2)
OA=OC
OB=OA
=>OC=OB
b: Từ (1), (2) suy ra góc BOC=2*(góc xOA+góc yOA)
=2*góc xOy=180 độ
=>B,O,C thẳng hàng
CM
5 tháng 1 2020
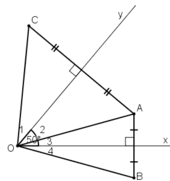
a) + B đối xứng với A qua Ox
⇒ Ox là đường trung trực của AB
⇒ OA = OB (1)
+ C đối xứng với A qua Oy
⇒ Oy là đường trung trực của AC
⇒ OA = OC (2)
Từ (1) và (2) suy ra OB = OC (= OA)
b) + ΔOAC cân tại O có Oy là đường trung trực
⇒ Oy đồng thời là đường phân giác
+ ΔOAB cân tại O có Ox là đường trung trực
⇒ Ox đồng thời là đường phân giác
9 tháng 11 2021
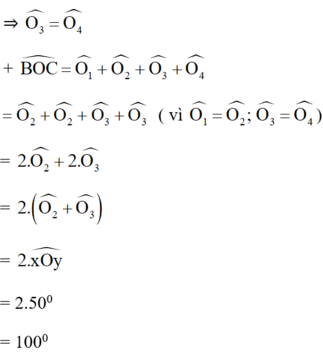
a: Ta có: B đối xứng với A qua Ox
nên OA=OB(1)
Ta có: C đối xứng với A qua Oy
nên OA=OC(2)
Từ (1) và (2) suy ra OB=OC
a: A và B đối xứng nhau qua Ox
nên OA=OB(1)
Ta có: A và C đối xứng nhau qua Oy
nên OA=OC(2)
Từ (1) và (2) suy ra OB=OC