Hình vuông ABCD có A(2;1), C(4;3). Tọa độ của đỉnh B có thể là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


25.
\(\lim\dfrac{3.5^n+7.7^n+9}{6.5^n+9.7^n-3}=\lim\dfrac{7^n\left[3\left(\dfrac{5}{7}\right)^n+7+9.\left(\dfrac{1}{7}\right)^n\right]}{7^n\left[6\left(\dfrac{5}{7}\right)^n+9-3\left(\dfrac{1}{7}\right)^n\right]}\)
\(=\lim\dfrac{3\left(\dfrac{5}{7}\right)^n+7+9\left(\dfrac{1}{7}\right)^n}{6\left(\dfrac{5}{7}\right)^n+9-3\left(\dfrac{1}{7}\right)^n}=\dfrac{3.0+7+9.0}{6.0+9-3.0}=\dfrac{7}{9}\)
26.
\(\lim\left(n-\sqrt{n^2-4n}\right)=\lim\dfrac{\left(n-\sqrt{n^2-4n}\right)\left(n+\sqrt{n^2-4n}\right)}{n+\sqrt{n^2-4n}}\)
\(=\lim\dfrac{4n}{n+\sqrt{n^2-4n}}=\lim\dfrac{4n}{n\left(1+\sqrt{1-\dfrac{4}{n}}\right)}\)
\(=\lim\dfrac{4}{1+\sqrt{1-\dfrac{4}{n}}}=\dfrac{4}{1+\sqrt{1-0}}=2\)
26.
\(u_1=5\)
\(u_n=405=u_1.q^{n-1}\Rightarrow q^{n-1}=\dfrac{405}{5}=81\)
\(\Rightarrow q^n=81q\)
Do \(S_n=\dfrac{u_1\left(1-q^n\right)}{1-q}\Rightarrow605=\dfrac{5\left(1-81q\right)}{1-q}\)
\(\Rightarrow605-605q=5-405q\)
\(\Rightarrow q=3\)

Xét dãy số \(u_n=S_{A_nB_nC_nD_n}\). Ta có \(u_1=a^2\)
Ta xét hình vuông có cạnh \(x\) (diện tích là \(x^2\)). Khi đó nửa độ dài đường chéo của hình vuông này sẽ là \(\dfrac{x}{\sqrt{2}}\). Khi đó diện tích của hình vuông mới là \(\left(\dfrac{x}{\sqrt{2}}\right)^2=\dfrac{x^2}{2}\) bằng 1 nửa diện tích hình vuông ban đầu. Như vậy, ta có mối quan hệ truy hồi: \(u_{n+1}=2u_n\). Dễ thấy đây là một cấp số nhân.
Ta có \(\left(u_n\right):\left\{{}\begin{matrix}u_1=a^2\\u_{n+1}=2u_n\end{matrix}\right.\)
\(\Rightarrow S_n=\sum\limits^{\infty}_{i=1}u_i=a^2\left(\sum\limits^{\infty}_{i=0}\dfrac{1}{2^i}\right)=2a^2\)
(Đẳng thức quen thuộc \(\sum\limits^{\infty}_{i=0}\dfrac{1}{2^i}=2\))
Cho \(S_n=8\) \(\Rightarrow2a^2=8\Leftrightarrow a=2\).
Vậy \(a=2\) thỏa mãn ycbt.

a.
\(SA\perp\left(ABCD\right)\Rightarrow AB\) là hình chiếu vuông góc của SB lên (ABCD)
\(\Rightarrow\widehat{SBA}=\left(SB;\left(ABCD\right)\right)\)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\dfrac{\sqrt{2}}{2}\Rightarrow\widehat{SBA}\approx35^016'\)
Tương tự \(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}=\left(SC;\left(ABCD\right)\right)\)
\(AC=\sqrt{AD^2+DC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)
b.
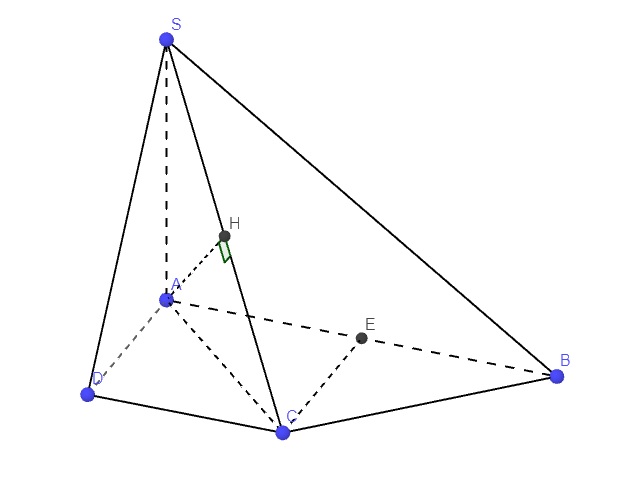
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AB\\AB\perp AD\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\)
\(\Rightarrow\left(AH;\left(SAD\right)\right)=90^0-\left(AH;AB\right)=90^0-\widehat{HAB}\)
Gọi E là trung điểm AB \(\Rightarrow ADCE\) là hình vuông \(\Rightarrow\widehat{ACE}=45^0\)
Tam giác BCE vuông cân tại E (do \(EB=EC=a\)) nên \(\widehat{ECB}=45^0\)
\(\Rightarrow\widehat{ACB}=90^0\) hay \(BC\perp AC\Rightarrow BC\perp\left(SAC\right)\) (do \(SA\perp BC\))
\(\Rightarrow BC\perp AH\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp BH\)
Hay tam giác ABH vuông tại H
\(AH=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=a\)
\(\Rightarrow cos\widehat{HAB}=\dfrac{AH}{AB}=\dfrac{1}{2}\Rightarrow\widehat{HAB}=60^0\)
\(\Rightarrow\widehat{HAB}=60^0\Rightarrow\left(AH;\left(SAD\right)\right)=30^0\)
Theo cmt \(BC\perp\left(SAC\right)\Rightarrow\left(SB;\left(SAC\right)\right)=\widehat{BSC}\)
\(SC=\sqrt{SA^2+AC^2}=2a\) ; \(SB=\sqrt{SA^2+AB^2}=a\sqrt{6}\)
\(\Rightarrow cos\widehat{BSC}=\dfrac{SC}{SB}=\dfrac{\sqrt{6}}{3}\Rightarrow\widehat{BSC}\approx35^016'\)

Chọn A.
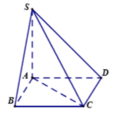
Vì SA vuông góc với đáy nên góc (SC,(ABCD)) = SCA.
Trong hình vuông ABCD có: AC = a 2 theo giả thiết, SA = a 2 => tam giác SAC vuông cân tại A
=> góc SCA = 45 °

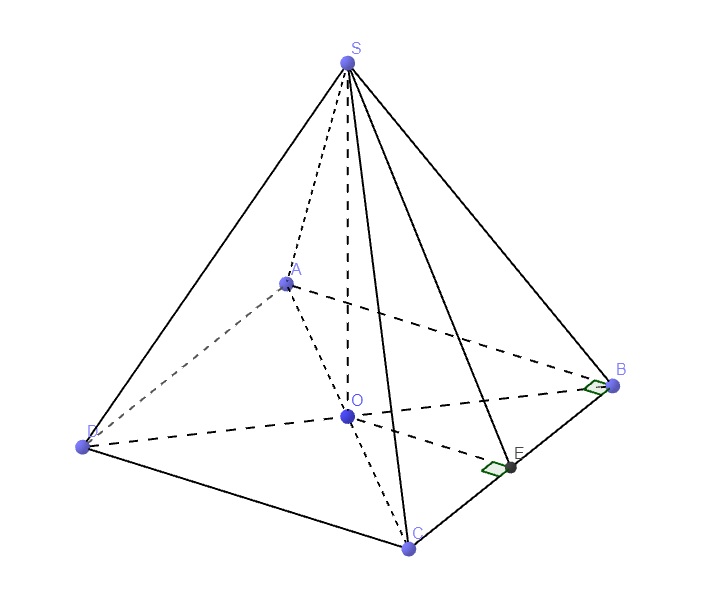
Gọi E là trung điểm BC \(\Rightarrow OE\) là đường trung bình tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}OE=\dfrac{1}{2}AB=\dfrac{a}{2}\\OE||AB\Rightarrow OE\perp BC\end{matrix}\right.\)
\(SO\perp\left(ABCD\right)\Rightarrow SO\perp BC\)
\(\Rightarrow BC\perp\left(SEO\right)\)
Mà \(BC=\left(SBC\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SEO}\) là góc giữa (SBC) và (ABCD)
\(tan\widehat{SEO}=\dfrac{SO}{OE}=\sqrt{3}\Rightarrow\widehat{SEO}=60^0\)

144 = 12 x 12
Vậy cạnh hình vuông có diện tích gấp 2 lần cạnh hình vuông ABCD là: 12m
Cạnh hình vuông ABCD là 12 : 2 = 6 m
Cạnh hình vuông cần tính là 6 x 3 = 18 m
Diện tích hình vuông đó là: 18 x 18 = 324 m2
Kí hiệu : Hình vuông có cạnh gấp 2 lần cạnh hình vuông ABCD là DEFG.
Hình vuông có cạnh gấp 3 lần cạnh hình vuông ABCD là MNPQ.
Giải.
Cạnh của hình vuông DEFG là 12cm (vì 12 x 12 = 144 cm2)
Cạnh của hình vuông ABCD là :
12 : 2 = 6(cm)
Cạnh của hình vuông MNPQ là :
6 x 3 = 18(cm)
Diệ tích hình vuông MNPQ là :
18 x 18 = 324 (cm2)
Đáp số : ...

Đáp án: B
A(2;1), C(4;3) ⇒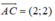
Gọi I là trung điểm của của AC ⇒ I(3;2)
Đường chéo BD là đường thẳng đi qua I và có vecto pháp tuyến là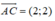
BD: 2(x - 3) + 2(y - 2) = 0 ⇔ x + y - 5 = 0
Thay tọa độ các điểm vào đường thẳng BD ta thấy tọa độ điểm ở đáp án B thỏa mãn phương trình đường thẳng BD.