Đường thẳng Δ đi qua M(x0; y0) và nhận vectơ 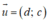 làm vectơ chỉ phương có phương trình là:
làm vectơ chỉ phương có phương trình là:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

CM
15 tháng 8 2019
Chọn D.
Phương trình tổng quát của đường thẳng Δ đi qua M(x0;y0) nhận 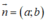 là VTPT là: a.(x - x0) + b.(y - y0) = 0
là VTPT là: a.(x - x0) + b.(y - y0) = 0

CM
3 tháng 6 2018
Chọn B.
Khoảng cách từ điểm M(x0;y0)đường thẳng Δ: ax + by + c = 0 được tính theo công thức:
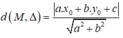

25 tháng 7 2021
\(\Delta\) đi qua M(1,-1) có hệ số góc k
=> \(\Delta:y=k\left(x-1\right)-1=kx-k-1\)
\(\Delta\) song song d: \(y=\dfrac{1}{2}x+\dfrac{1}{2}\) \(=>k=\dfrac{1}{2}\)
\(\Delta:y=\dfrac{1}{2}x-\dfrac{3}{2}\)

11 tháng 1 2016
a)Phương Trình của đường thẳng ox là :y=0x+0 .
b)Phương Trình của đường thẳng oy là x=0
Chọn A.
Phương trình tham số của đường thẳng Δ là: