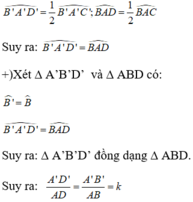Chứng minh rằng : Nếu 2 tam giác đồng dạng thì tỉ số 2 bán kính đường tròn ngoại tiếp bằng tỉ số đồng dạng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



AB/sinC=2R
A'B'/sinC'=2R'
mà AB/A'B'=k
và goc C=góc C'
nên 2R/2R'=AB/A'B'=k
=>R/R'=k(Đpcm)

Hai tam giác được gọi là đồng dạng nếu một trong chúng bằng với một tam giác nhận được từ tam giác kia sau một phép vị tự. Các điều kiện cần và đủ để hai tam giác đồng dạng:

a) BE // DC => ∆BEF ∽ ∆CDF
AD // BF => ∆ADE ∽ ∆BFE.
Do đó: ∆ADE ∽ ∆CFD
b) BE = AB - AE = 12 - 8 = 4cm
∆ADE ∽ ∆BFE => \(\dfrac{AE}{BE}=\dfrac{AD}{BF}=\dfrac{DE}{FD}\)
=> \(\dfrac{8}{4}=\dfrac{7}{BF}=\dfrac{10}{EF}\)
=> BF = 3,5 cm.
EF = 5 cm.

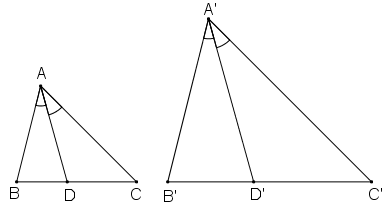
Gọi AD và A’D' lần lượt là hai đường phân giác của ΔABC và ΔA'B'C'.
+) Lại có; AD, A’D’ lần lượt là phân giác của góc A và góc A’ nên:
( Bạn tự kẻ hình nhé!!! )
Gọi AD và A’D' lần lượt là hai đường phân giác của ΔABC và ΔA'B'C'
Tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k nên:
\(\widehat{B'}=\widehat{B}\), \(\widehat{A'}=\widehat{A}\), \(\frac{A'B'}{AB}=k\)
Lại có; AD, A’D’ lần lượt là phân giác của góc A và góc A’ nên:
\(\widehat{B'A'D'}=\frac{1}{2}\widehat{B'A'C'}\), \(\widehat{BAD}=\frac{1}{2}\widehat{BAC}\)
\(\Rightarrow\widehat{B'A'D'}=\widehat{BAD}\)
Xét tam giác A'B'D' và tam giác ABD:
\(\widehat{B'}=\widehat{B}\)
\(\widehat{B'A'D'}=\widehat{BAD}\)
\(\Rightarrow\)tam giác A'B'D' đồng dạng với tam giác ABD
\(\Rightarrow\frac{A'D'}{AD}=\frac{A'B'}{AB}=k\)

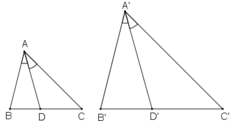
Gọi AD và A’D' lần lượt là hai đường phân giác của ΔABC và ΔA'B'C'.
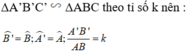
+) Lại có; AD, A’D’ lần lượt là phân giác của góc A và góc A’ nên: