Gieo một con xúc xắc 2 lần. Xác suất để mặt 6 chấm không xuất hiện là A. B. C. D....
Đọc tiếp
Gieo một con xúc xắc 2 lần. Xác suất để mặt 6 chấm không xuất hiện là
A. 
B. 
C. 
D. 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 9 2017
Đáp án A
Số phần tử của không gian mẫu: n Ω = 6 .6 = 36 .
Gọi A là biến cố mặt 6 chấm không xuất hiện.
Khi đó n A = 5 .5 = 25 ⇒ P A = n A n Ω = 25 36 .
MN
18 tháng 4 2021
a) Nếu gieo một xúc xắc 11 lần liên tiếp, có 5 lần xuất hiện mặt 2 chấm thì xác suất thực nghiệm xuất hiện mặt 2 chấm bằng: \(\dfrac{5}{11}\)
b) Nếu gieo một xúc xắc 14 lần liên tiếp, có 3 lần xuất hiện mặt 6 chấm thì xác suất thực nghiệm xuất hiện mặt 6 chấm bằng: \(\dfrac{3}{14}\)
NK
10 tháng 5 2023
Vì gieo xúc xắc 20 lần và có 6 lần xuất hiện mặt 3 chấm nên ta có phân số: `6/20`.
Từ đó, ta có: \(\dfrac{6}{20}=\dfrac{3}{10}=0,3\).
Vậy `0,3` là xác suất thực nghiệm xuất hiện mặt 3 chấm.
Do đó, ý B là ý đúng.
VV
0
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 4 2023
Có 2 trường hợp thuận lợi là các mặt 4 ,6
Do đó xác suất là: \(\dfrac{2}{6}=\dfrac{1}{3}\)
30 tháng 4 2023
a: n(omega)=6
n(A)=3
=>P(A)=3/6=1/2
b: n(B)=5
=>P(B)=5/6
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
Tập hợp gồm các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc là:
A = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}.
Số phần tử của tập hợp A là 6.
a) Có bốn kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là ước của 6” là: mặt 1 chấm, mặt 2 chấm, mặt 3 chấm, mặt 6 chấm.
Vì thế, xác suất của biến cố trên là \(\dfrac{4}{6} = \dfrac{2}{3}\).
b) Có hai kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chia 3 dư 2” là: mặt 2 chấm, mặt 5 chấm.
Vì thế, xác suất của biến cố trên là \(\dfrac{2}{6} = \dfrac{1}{3}\).
13 tháng 4 2023
a: A={(1;1); (1;2); ...; (1;6)}
=>n(A)=6
P(A)=6/36=1/6
b: B={(1;4); (2;3); (3;2); (4;1)}
=>P(B)=4/36=1/9
c: C={(3;1); (4;2); (5;3); (6;4)}
=>P(C)=4/36=1/9
d: D={(1;3); (1;5); (1;1); (3;5); (3;1); (3;3); (5;3); (5;1); (5;5)}
=>P(D)=9/36=1/4
Đáp án A
Số phần tử của không gian mẫu: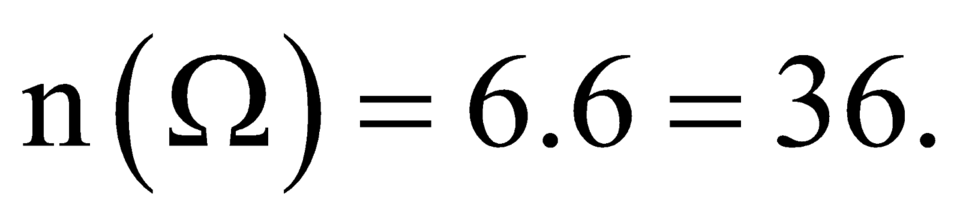
Gọi A là biến cố mặt 6 chấm không xuất hiện.