Cho lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đáy bằng a. Gọi M, N, P là trung điểm của các cạnh AD, DC, A’D’. Tính khoảng cách giữa CC’ và mặt phẳng (MNP)?
A. a 2 4
B. a 3 3
C. a 2
D. a 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 12 2018
Do tam giác ABC đều cạnh a và M là trung điểm BC cho nên A M ⊥ B C và A M = a 3 2 .
A M ⊥ B C và A A ' ⊥ B C ⇒ A ' M ⊥ B C
⇒ Góc giữa hai mặt phẳng (A’BC) và (ABC) là A ' M A ^ = 60 o
Tam giác A’AM vuông góc tại A nên A A ' = A M . tan 60 o = a 3 2 . 3 = 3 a 2
Diện tích hình chữ nhật BB’C’C là S B B ' C ' C = B B ' . B C = 3 a 2 2
A M ⊥ B C và A M ⊥ B B ' ⇒ A M ⊥ B B ' C ' C
Thể tích khối chóp A.BB’C’C là: V = 1 3 . S B B ' C ' C . A M = 1 3 . 3 a 2 2 . a 3 2 = a 3 3 4 (đvtt).
Đáp án A
CM
4 tháng 12 2019
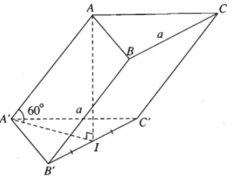
a) Gọi I là trung điểm của cạnh B'C'. Theo giả thiết ta có AI ⊥ (A'B'C') và ∠ A A ′ I = 60 ο . Ta biết rằng hai mặt phẳng (ABC) và (A'B'C') song song với nhau nên khoảng cách giữa hai mặt phẳng chính là khoảng cách AI.
Do đó
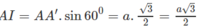
b)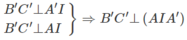 
⇒ B′C′ ⊥ AA′
Mà AA′ // BB′ // CC′ nên B’C’ ⊥ BB’
Vậy mặt bên BCC’B’ là một hình vuông vì nó là hình thoi có một góc vuông.
CM
1 tháng 1 2019
Đáp án A
Khoảng cách giữa hai mặt đáy là h = AH = A’H.tan A A ' H ^ = a 3 2 . tan 30 0 = a 2
Chọn A.
- Ta có: