Cho tứ diện ABCD có các cạnh AB, BC, BD vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng?
A. Góc giữa AC và (ABD) là góc CAB.
B. Góc giữa AD và (ABC) là góc ADB.
C. Góc giữa CD và (ABD) là góc CBD.
D. Góc giữa AC và (BCD) là góc ACD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
Do \(AB=AC\Rightarrow\Delta ABC\) cân tại A
\(\Rightarrow AM\) là trung tuyến đồng thời là đường cao
\(\Rightarrow AM\perp BC\) (1)
Mà \(\left\{{}\begin{matrix}AD\perp AB\left(gt\right)\\AD\perp AC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AD\perp\left(ABC\right)\Rightarrow AD\perp BC\) (2)
(1);(2) \(\Rightarrow BC\perp\left(ADM\right)\)
b.
Từ A kẻ \(AE\perp DM\) (E thuộc DM)
Do \(BC\perp\left(ADM\right)\Rightarrow BC\perp AE\)
\(\Rightarrow AE\perp\left(BCD\right)\Rightarrow AE=d\left(A;\left(BCD\right)\right)\)
\(BC=\sqrt{AB^2+AC^2}=5\sqrt{2}\Rightarrow AM=\dfrac{1}{2}BC=\dfrac{5\sqrt{2}}{2}\)
Hệ thức lượng trong tam giác vuông ADM:
\(AE=\dfrac{AD.AM}{\sqrt{AD^2+AM^2}}=\dfrac{5\sqrt{3}}{3}\)
c.
Do \(AD\perp\left(ABC\right)\) theo cmt \(\Rightarrow AM\) là hình chiếu vuông góc của DM lên (ABC)
\(\Rightarrow\widehat{DMA}\) là góc giữa DM và (ABC)
\(tan\widehat{DMA}=\dfrac{AD}{AM}=\sqrt{2}\Rightarrow\widehat{DMA}\approx54^044'\)

Góc giữa AC với mặt phẳng (ABD) là góc KAC vì CK ⊥ (ABD) nên AK là hình chiếu của AC trên mặt phẳng (ABD).
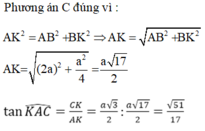
Đáp án C
Chọn A
- Ta có:
- Suy ra AB là hình chiếu của AC lên (ABD).
- Do đó: