Phần I: Trắc nghiệm
Cho hình hộp ABCD.A'B'C'D' có tâm O. Gọi I là tâm hình bình hành ABCD. Đặt A C ' → = u → , C A ' → = v → , B D ' → = x → , D B ' → = y → . Khẳng định nào sau đây đúng?
A. 2 O I → = 1 2 u → + v → + x → + y →
B. 2 O I → = - 1 2 u → + v → + x → + y →
C. 2 O I → = 1 4 u → + v → + x → + y →
D. 2 O I → = - 1 4 u → + v → + x → + y →

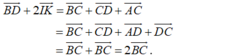
 đều song song hoặc trùng với mặt phẳng (ABCD). Do đó, theo định nghĩa sự đồng phẳng của các vectơ, ba vectơ trên đồng phẳng.
đều song song hoặc trùng với mặt phẳng (ABCD). Do đó, theo định nghĩa sự đồng phẳng của các vectơ, ba vectơ trên đồng phẳng.
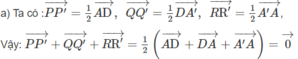
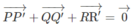
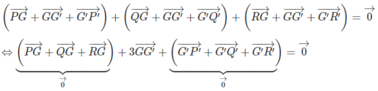
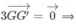 G trùng với G'
G trùng với G'

Chọn D.
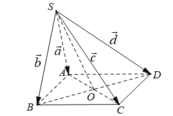
- Ta phân tích: