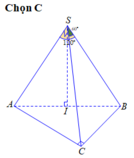
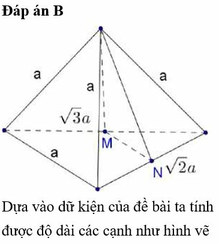
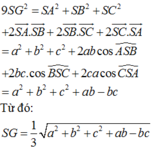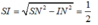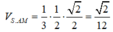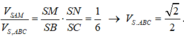Cho hình chóp S.ABC có BSC= 120 o , CSA= 60 o , ASB= 90 o , SA=SB=SC Gọi I là hình chiếu vuông góc của S lên mp (ABC) Chọn khẳng định đúng trong các khẳng định sau?
A. I là trung điểm của AB
B. I là trung điểm của BC
C. I là trọng tâm của tam giác ABC
D. I là trung điểm của AC