Tìm khoảng nghịch biến của hàm số y = x 3 + 3 x 2 + 2
A. (2;+∞)
B. (0;2)
C. (-2;0)
D. (-∞;2)∪(0;+∞)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Từ đồ thị ta thấy hàm số xác định trên [-3;7]
+) Trên khoảng (-3; 1): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (-3; 1).
+) Trên khoảng (1; 3): đồ thị có dạng đi xuống từ trái sang phải nên hàm số này nghịch biến trên khoảng (1; 3).
+) Trên khoảng (3; 7): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (3; 7).
b) Xét hàm số \(y = 5{x^2}\) trên khoảng (2; 5).
Lấy \({x_1},{x_2} \in (2;5)\) là hai số tùy ý sao cho \({x_1} < {x_2}\).
Do \({x_1},{x_2} \in (2;5)\) và \({x_1} < {x_2}\) nên \(0 < {x_1} < {x_2}\), suy ra \({x_1}^2 < {x_2}^2\) hay \(5{x_1}^2 < 5{x_2}^2\)
Từ đây suy ra \(f({x_1}) < f({x_2})\)
Vậy hàm số đồng biến (tăng) trên khoảng (2; 5).

1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)

a: y'=-4x^3+8*2x
=-4x^3+16x
y'>0 khi -4x^3+16x>0
=>-4x(x^2-4)>0
=>x(x^2-4)<0
=>x<-2; 0<x<2
Vậy: Khi x<-2 hoặc 0<x<2 thì hàm số đồng biến
y'<0 khi -4x^3+16x<0
=>-2<x<0; x>2
Vậy: Khi -2<x<0 hoặc x>2 thì hàm số nghịch biến
b: y'=4x^3
y'>0 khi x>0
=>Khi x>0 thì hàm số đồng biến
y'<0 khi 4x^3<0
=>x<0
=>Khi x<0 thì hàm số nghịch biến

Vẽ đồ thi \(y = 3{x^2} - 10x + 7\)
- Có đỉnh \(\)\(I\left( {\frac{5}{3}; - \frac{4}{3}} \right)\), có trục đối xứng là đường thẳng \(x = \frac{5}{3}\)
- Đi qua điểm \((0;7);\left( {1;0} \right)\)

- Hàm số nghịch biến trên khoảng \(\left( { - \infty ;\frac{5}{3}} \right)\); đồng biến trên khoảng \(\left( {\frac{5}{3}; + \infty } \right)\)
- Giá trị nhỏ nhất của hàm số là tại điểm có tọa độ \(\left( {\frac{5}{3}; - \frac{4}{3}} \right)\)

1: TXĐ: D=R\{3}
\(y=\dfrac{x^2-6x+10}{x-3}\)
=>\(y'=\dfrac{\left(x^2-6x+10\right)'\left(x-3\right)-\left(x^2-6x+10\right)\left(x-3\right)'}{\left(x-3\right)^2}\)
=>\(y'=\dfrac{\left(2x-6\right)\left(x-3\right)-\left(x^2-6x+10\right)}{\left(x-3\right)^2}\)
=>\(y'=\dfrac{2x^2-12x+18-x^2+6x-10}{\left(x-3\right)^2}\)
=>\(y'=\dfrac{x^2-6x+8}{\left(x-3\right)^2}\)
Đặt y'<=0
=>\(\dfrac{x^2-6x+8}{\left(x-3\right)^2}< =0\)
=>\(x^2-6x+8< =0\)
=>(x-2)(x-4)<=0
=>2<=x<=4
Vậy: Khoảng đồng biến là [2;3) và (3;4]

a: y'=3x^2-3*2x=3x^2-6x=3x(x-2)
y'>0 khi x(x-2)>0
=>x>2 hoặc x<0
=>Khi x>2 hoặc x<0 thì hàm số đồng biến
y'<0 khi x(x-2)<0
=>0<x<2
=>Khi 0<x<2 thì hàm số nghịch biến
b: y'=-3x^2+3
y'>0 khi -3x^2+3>0
=>-3x^2>-3
=>x^2<1
=>-1<x<1
Khi -1<x<1 thì hàm số đồng biến
y'<0 khi x^2>1
=>x>1 hoặc x<-1
Vậy: Khi x>1 hoặc x<-1 thì hàm số nghịch biến

a) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - 1; + \infty } \right)\) nên hàm số đồng biến trong khoảng \(\left( { - 1; + \infty } \right)\). Trong khoảng \(\left( { - \infty ; - 1} \right)\) thì hàm số nghich biến.
Bảng biến thiên:
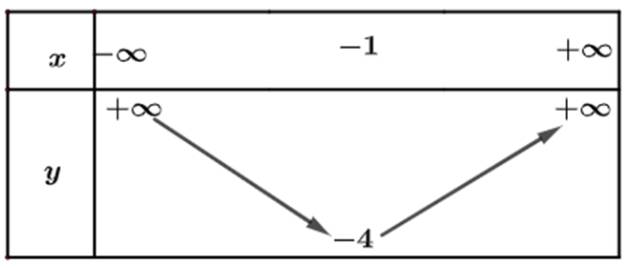
b) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - \infty ;1} \right)\) nên hàm số đồng biến trong khoảng \(\left( { - \infty ;1} \right)\). Trong khoảng \(\left( {1; + \infty } \right)\) thì hàm số nghịch biến.
Bảng biến thiên:
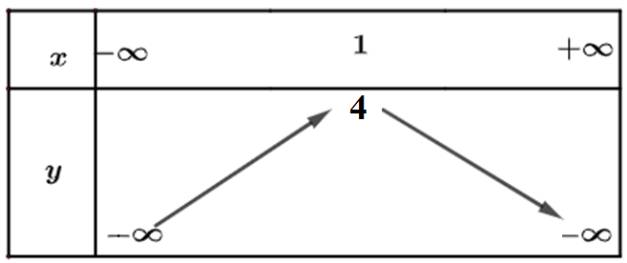
Đáp án C
Phương pháp:
Xác định khoảng mà tại đó y' ≤ 0, dấu “=” xảy ra ở hữu hạn điểm.
Cách giải:
Hàm số nghịch biến trên khoảng (-2;0)