Biết rằng nghịch đảo của số phức z ≠ 0 bằng số phức liên hợp của z. Kết luận nào sau đây đúng?
A. ![]() .
.
B.![]() .
.
C.![]() là một số thuần ảo.
là một số thuần ảo.
D.![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(z=x+y.i\) \(\Rightarrow\overline{z}=x-yi\)
Theo bài ra ta có:
\(\frac{1}{z}=\overline{z}\Leftrightarrow\frac{1}{x+yi}=x-yi\)
\(\Leftrightarrow\left(x+yi\right)\left(x-yi\right)=1\Leftrightarrow x^2+y^2=1\)
\(\Rightarrow\left|z\right|=1\)

Đáp án D.
Đặt z = a + b i a ; b ∈ ℝ
Theo đề bài ta có
1 z = z ¯ ⇔ 1 a + b i = a − b i ⇔ a + b i a − b i = 1 ⇔ a 2 + b 2 = 1
⇒ z = 1

Chọn D.
Giả sử z = a+ bi thì ![]() khi và chỉ khi a = b - 4 (1)
khi và chỉ khi a = b - 4 (1)
Với a ≠ 0 hoặc b ≠ 1, ta có:
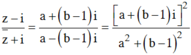
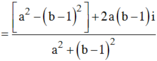
Vì ![]() là số thuần ảo nên a2 - ( b - 1) 2 = 0 khi và chỉ khi a = b - 1 hoặc a = 1 - b
là số thuần ảo nên a2 - ( b - 1) 2 = 0 khi và chỉ khi a = b - 1 hoặc a = 1 - b
Kết hợp (1) ta có a = -3/2 và b = 5/2.
Vậy số phức đó là 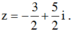

Đáp án B.
Ta có: Phần thực: –4, phần ảo: –3
![]()
Hai ý (3) và (4) sai.