Một công ty sản xuất một loại cốc giấy hình nón không nắp ( nghĩa là không có hình tròn đáy) có thể tích 27cm3. Với chiều cao h và bán kính đáy là r. Tìm r để lượng giấy tiêu thụ ít nhất:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Ta có x = k . R là chu vi đường tròn đáy của khối nón ⇒ k . R = 2 π r ⇒ r = k . R 2 π
Độ dài đường sinh của khối nón chính là bán kính R ⇒ l = R = r 2 + h 2 ⇒ h = R 2 − r 2
Thể tích của khối nón là:
V = 1 3 π r 2 h = 1 3 π . r 2 . R 2 − r 2 ⇔ V 2 = π 2 9 . r 4 . R 2 − r 2 . 1
Theo bất đẳng thức Cosi, ta được r 2 . R 2 − r 2 = 4. r 2 2 . r 2 2 . R 2 − r 2 ≤ 4 R 6 27 2
Từ (1), (2) suy ra:
V = π 2 9 . 4 R 6 27 = 4 π 2 243 R 6 ⇒ V ≤ 2 π 9 3 R 3
Dấu “=” xảy ra khi:
⇔ r 2 2 = R 2 − r 2 ⇔ R 2 = 3 2 r 2 = 3 2 . k 2 R 2 4 π 2 ⇒ k 2 = 8 π 2 3 ⇒ k ≃ 5 , 13

Đáp án B
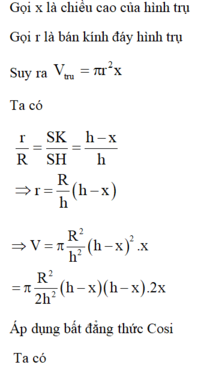
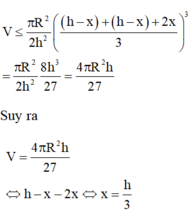
Vậy khi vị trí mặt phẳng α cách đáy hình nón một khoảng h 3 thì khối trụ có diện tích lớn nhất

Đáp án C
Thể tích của khối nón là V n = 1 3 π r 2 h 1 và độ dài đường sinh là l = r 2 + h 2
Thể tích của khối trụ là V t = π r 2 h 2 = 1 3 π r 2 h
Vậy thể tích cái nắp là V = V n + V t = 2 3 π r 2 h
Mặt khác l =1,25
⇒ r 2 + h 2 = 25 4 ⇔ r 2 = 25 4 − h 2
khi đó:
V = 2 3 π h 25 4 − h 2 ≤ 2 π 3 . 125 12 3
Ta có:
V 2 = 4 9 π 2 h 2 25 4 − h 2 2 ≤ 2 9 π 2 . 25 4 − h 2 . 25 4 − h 2 2 9 π 2 . 25 4 − h 2 . 25 4 − h 2 ≤ 2 π 2 9 . 25 4 + 25 4 3 3
Dấu bằng xảy ra khi:
2 h 2 = 25 4 − h 2 ⇔ h 2 = 25 12 ⇒ h = 5 2 3
Dấu “=” xảy ra khi:
2 h 2 = 25 4 − h 2 ⇔ h 2 = 25 12 ⇒ h = 5 2 3 ⇒ r = 25 4 − h 2 = 5 6 6 ⇒ r + h ≃ 348 c m

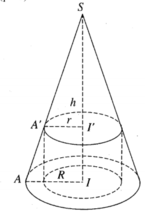
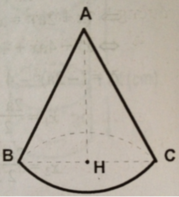
V H ' lớn nhất khi f(r) = r 2 (R - r) (với 0 < r < R) là lớn nhất. Khảo sát hàm số f(r), với 0 < r < R. Ta có f'(r) = 2Rr - 3 r 2 = 0, khi r = 0 (loại), hoặc r = 2R/3. Lập bảng biến thiên ta thấy f(r) đạt cực đại tại r = 2R/3.
Khi đó ![]()

Chọn C.
Phương pháp:
Sử dụng các công thức tính thể tích:

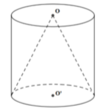
Nhận xét: Hai khối nón và khối trụ có cùng chiều cao h và cùng bán kính đáy bằng r.
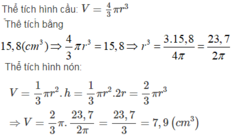


Chọn C.