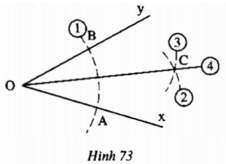
1, Cho góc nhọn xOy, vẽ đường tròn tâm O bán kính 3 cm cắt Ox ở A, cắt Oy ở B. Vẽ đường tròn tâm A và tâm B cùng bán kính 4 cm cắt nhau tại điểm M nằm trong góc xOy. Chứng minh OM là tia phân giác của góc xOy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 3 2016
xem hình vẽ:
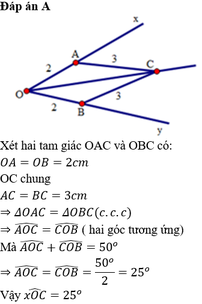
Nối BC, AC.
∆OBC và ∆OAC có:
OB=OA(Bán kính)
BC=AC(gt)
OC cạnh chung
nên∆OBC = ∆OAC(c.c.c)
Nên BOC=AOC (hai góc tương ứng)
Vậy OC là tia phân giác xOy.
19 tháng 9 2023
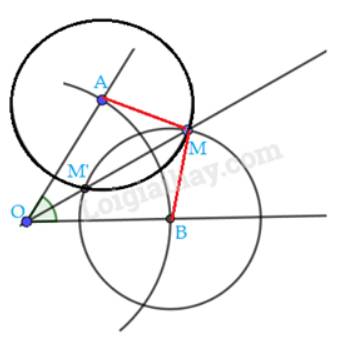
Ta có: AM = bán kính đường tròn tâm A
BM = bán kính đường tròn tâm B
Mà 2 đường tròn này có bán kính bằng nhau
Do đó, AM = BM
Xét \(\Delta \)OAM và \(\Delta \)OBM có:
OA = OB( = bán kính đường tròn tâm O)
MA = MB (cmt)
OM chung
\( \Rightarrow \) \(\Delta \)OAM = \(\Delta \)OBM ( c.c.c)
\( \Rightarrow \) \(\widehat {AOM} = \widehat {BOM}\) ( 2 góc tương ứng)
Mà OM nằm giữa 2 tia OA và OB
\( \Rightarrow \) OM là tia phân giác của góc AOB.
CM
19 tháng 3 2019
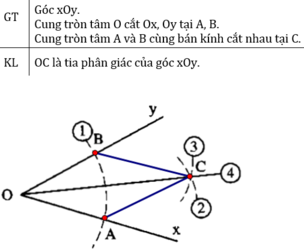
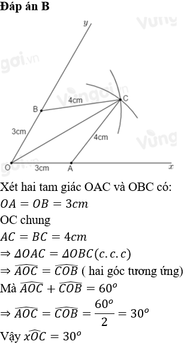
Nối BC, AC
ΔOBC và ΔOAC có:
OB = OA (bán kính)
AC = BC (gt)
OC cạnh chung
Nên ΔOBC = ΔOAC (c.c.c)
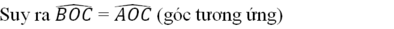
nên OC là tia phân giác của góc xOy.