Hàm số f x = x 2 − 1 khi x ≤ 1 x + m khi x > 1 liên tục tại điểm x 0 = 1 khi m nhận giá trị
A. m = 1
B. m = 2
C. m bất kì
D. m = − 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Phương pháp: Hàm số y = f(x) liên tục tại ![]()
Cách giải: 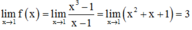
f(1) = 2m+1
Để hàm số liên tục tại x = 1
![]()

Ta có lim x → 1 − f x = lim x → 1 − m x + 1 = m + 1
lim x → 1 + f x = lim x → 1 + x 3 − x 2 x − 1 = lim x → 1 + x − 1 x 2 x − 1 = lim x → 1 + x 2 = 1
f(1) = n
Để hàm số liên tục tại x= 1 thì lim x → 1 − f x = lim x → 1 + f x = f 1
Suy ra: m + 1 = 1= n nên n = 1 và m = 0
Chọn đáp án D.
Đáp án D
Ta có lim x → 1 + f x = lim x → 1 + x 2 − 1 = 0 , lim x → 1 − f x = lim x → 1 − x + m = 1 + m , f 1 = 1 2 − 1 = 0
để hàm số liên tục tại x 0 = 1 thì lim x → 1 + f x = lim x → 1 − f x = f 1 ⇔ 0 = 1 + m ⇔ m = − 1