Hàm số nào sau đây nghịch biến trên mỗi khoảng xác định của nó?
A. y = x - 2 - x + 2
B. y = x - 2 x + 2
C. y = - x + 2 x + 2
D. y = x + 2 - x + 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án: D.
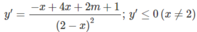
⇔ ∆ ′ = 2m + 5 ≤ 0
dấu “=” xảy ra nhiều nhất tại hai điểm, nên hàm số nghịch biến trên các khoảng (- ∞ ; 2)
và (2; + ∞ ) khi m ≤ −5/2.

\(\dfrac{\sqrt{3}}{2}< 1;\dfrac{\sqrt[3]{26}}{3}< 1;\pi>1;\dfrac{\sqrt{15}}{4}< 1\)
Hàm số đồng biến là: \(log_{\pi}x\)
Hàm số nghịch biến là: \(\left(\dfrac{\sqrt{3}}{2}\right)^x;\left(\dfrac{\sqrt[3]{26}}{3}\right)^x;log_{\dfrac{\sqrt{15}}{4}}x\)

Chọn: A
Xét đáp án A ta có:
![]()
và y ' = - 4 x + 2 2 < 0 ∀ x ∈ D
Vậy hàm số y = - x + 2 x + 2 nghịch biến trên mỗi khoảng xác định của nó.