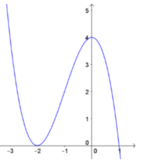
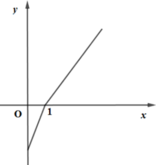
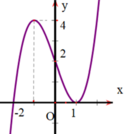
Cho hàm số xác định và có đạo hàm trên Đạo hàm của hàm số là có đồ thị như hình dưới
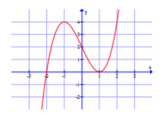
Khẳng định nào sau đây là khẳng định sai:
A. Hàm số nghịch biến trên khoảng ( - ∞ ; - 2 )
B. Hàm số đạt cực tiểu tại x=1
C. Hàm số đồng biến trên khoảng ( - 2 ; + ∞ )
D. Hàm số đạt cực tiểu tại x= -2

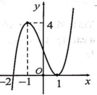

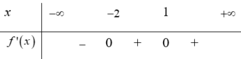

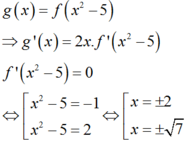


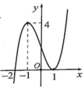
Đáp án B
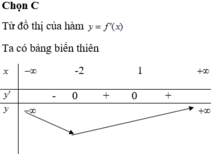
Dễ thấy y’ = 0 tại x = -2 và x = 1
Lại thấy y’ < 0 trên khoảng (-∞;2) và y’ ≥ 0 trên khoảng (-2;+∞)
Từ đó ta có bảng biến thiên