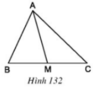
Cho tam giác ABC và đường trung tuyến AM (h.132). Chứng minh: SAMB = SAMC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
3 tháng 9 2019
Kẻ đường cao AH
Ta có: SAMB = 0.5.BM.AH
SAMC = 0.5.CM.AH
Mà BM = CM (gt)
Þ SAMB = SAMC (ĐPCM)
20 tháng 8 2023
a: Xét ΔMHB vuông tại H và ΔMKC vuông tại K có
MB=MC
góc HMB=góc KMC
=>ΔMHB=ΔMKC
=>HB=CK
b: Xét tứ giác BHCK có
BH//CK
BH=CK
Do đó BHCK là hình bình hành
=>BK//CH
7 tháng 6 2021
a, Xét \(\Delta ABC\left(\perp A\right)\) và \(\Delta HBA\left(\perp H\right)\) có \(\widehat{B}\) chung
b,\(\Delta ABC\sim\Delta HBA\) theo a
\(\Rightarrow\dfrac{AB}{HB}=\dfrac{BC}{AB}\Leftrightarrow AB^2=HB.BC\)
\(=4.\left(4+9\right)\)
\(\Rightarrow AB=2\sqrt{13}\) (cm)
Áp dụng định lí py-ta-go trong \(\Delta ABH\):
\(AH=\sqrt{AB^2-BH^2}=6\left(cm\right)\)
Vì \(AH=DE=6cm\)
c, Xét \(\Delta HBA\left(\perp H\right)\) và \(\Delta DHA\left(\perp D\right)\) có \(\widehat{A}\) chung
\(\Rightarrow\Delta HBA\sim\Delta DHA\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{AH}=\dfrac{AH}{AB}\Rightarrow AD.AB=AH^2\) \(\left(1\right)\)
Tương tự \(\Delta EHA\sim\Delta HCA\left(g.g\right)\)
\(\Rightarrow\dfrac{AE}{AH}=\dfrac{AH}{AC}\Rightarrow AE.AC=AH^2\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow AD.AB=AE.AC\)
-Chúc bạn học tốt-
10 tháng 11 2021
a, Vì \(\widehat{AEH}=\widehat{ADH}=\widehat{DAE}=90^0\) nên AEHD là hcn
Do đó AH=DE
b, Vì \(\widehat{HAB}=\widehat{MCA}\) (cùng phụ \(\widehat{CAH}\))
Mà \(\widehat{MCA}=\widehat{MAC}\) (do \(AM=CM=\dfrac{1}{2}BC\) theo tc trung tuyến ứng ch)
Vậy \(\widehat{HAB}=\widehat{MAC}\)
c, Gọi O là giao AM và DE
Vì AEHD là hcn nên \(\widehat{HAB}=\widehat{ADE}\Rightarrow\widehat{MAC}=\widehat{ADE}\)
Mà \(\widehat{ADE}+\widehat{AED}=90^0\left(\Delta AED\perp A\right)\) nên \(\widehat{MAC}+\widehat{ADE}=90^0\)
Xét tam giác AOE có \(\widehat{AOE}=180^0-\left(\widehat{MAC}+\widehat{ADE}\right)=90^0\)
Vậy AM⊥DE tại O
25 tháng 11 2022
a: Kẻ đường cao AH
\(S_{AMB}=\dfrac{1}{2}\cdot AH\cdot MB\)
\(S_{AMC}=\dfrac{1}{2}\cdot AH\cdot MC\)
mà MB=MC
nên \(S_{AMB}=S_{AMC}\)
MB=1/2BC
=>\(S_{AMB}=\dfrac{1}{2}\cdot AH\cdot\dfrac{1}{2}\cdot BC=\dfrac{1}{2}\cdot S_{ABC}\)
=>ĐPCM
b: Xét ΔABC có BC^2=AB^2+AC^2
nên ΔABC vuông tại A
AN=AC/2=4cm
\(S_{ANB}=\dfrac{1}{2}\cdot4\cdot6=2\cdot6=12\left(cm^2\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot6\cdot8=24\left(cm^2\right)\)
=>\(S_{BNC}=12\left(cm^2\right)\)
=>\(S_{BMN}=\dfrac{1}{2}\cdot12=6\left(cm^2\right)\)
5 tháng 3 2021
CM được \(\Delta\)ABC cân tại A (theo Cho tam giác ABC có đường tròn tiếp xúc với hai cạnh AB, AC và với hai trung tuyến BM, CN( M thuộc AC, N thuộc AB). Chứn... - Hoc24)
\(\Rightarrow\) AB = AC (t/c) (1)
Mà: M là trung điểm của AC; N là trung điểm của AB
\(\Rightarrow\) AM = AN (2)
Ta có: SAMB = SANC
\(\Rightarrow\) AM.MB = AN.NC
\(\Rightarrow\) \(\dfrac{AM}{AN}=\dfrac{NC}{MB}\)
Mà: AM = AN
\(\Rightarrow\) \(\dfrac{NC}{MB}=\dfrac{AM}{AM}=1\)
\(\Rightarrow\) NC = MB (3)
Cộng 2 vế của (1); (2); (3) ta được:
AM + MB + AB = AN + NC + AC (đpcm)
Chúc bn học tốt!
Kẻ đường cao AH.
Ta có:
Mà BM = CM (vì AM là trung tuyến)
⇒ SAMB = SAMC (đpcm).