Cho các điểm A(2; 3), B(9; 4), M(5; y) và P(x; 2).
a, Tìm y để tam giác AMB vuông tại M;
b, Tìm x để ba điểm A, B và P thẳng hàng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

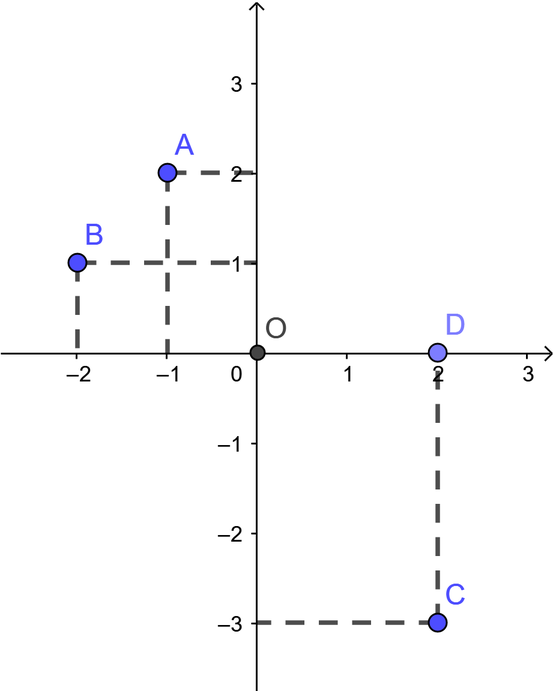
Biểu diễn các điểm trên hệ trục tọa độ Oxy ta thấy có hai điểm nằm trong góc phần tư thứ hai là A và B
Chọn đáp án C

Gọi C là điểm bất kì trong 97 điểm còn lại
Ba điểm A,B,C lập thành một nhóm.
Theo giả thiết một nhóm bao giờ cũng có thể chọn ra hai điểm có khoảng cách nhỏ hơn 1cm

Theo nguyên lí Điriclê thì phải có một đường tròn chứa ít nhất 49 điểm.
Thêm điểm A hoặc B nữa thì có một đường tròn chứa ít nhất 50 điểm.

Gọi \(M\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(x-1;y-2\right)\\\overrightarrow{BM}=\left(x+3;y-1\right)\\\overrightarrow{CM}=\left(x-4;y-2\right)\end{matrix}\right.\)
\(MA^2+MB^2=MC^2\)
\(\Leftrightarrow\left(x-1\right)^2+\left(y-2\right)^2+\left(x+3\right)^2+\left(y-1\right)^2=\left(x-4\right)^2+\left(y-2\right)^2\)
\(\Leftrightarrow x^2+y^2+12x-2y-5=0\)
\(\Rightarrow I\left(-6;1\right)\)
Vậy với M(5; 7) hoặc M(5; 0) thì tam giác ABM vuông tại M.
Vậy P(-5; 2)