Tính khoảng cách giữa hai cạnh đối trong một tứ diện đều cạnh a.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SG
1
PT
1
CM
14 tháng 9 2019
Đáp án B.
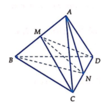
Gọi ABCD là tứ diện đều cạnh a.
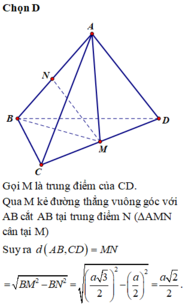
Gọi M là trung điểm của AB và N là trung điểm của CD.
Do NA=NB nên tam giác NAB cân ⇒ M N ⊥ A B .
Do MC=MD nên tam giác MCD cân ⇒ M N ⊥ C D .
Suy ra MN là đoạn vuông góc chung của AB và CD.
Tam giác BMN vuông tại M
⇒ M N = B N 2 - B M 2 = a 3 2 2 - a 2 2 = 2 a 2 4 = a 2 2 .
Vậy d ( A B , C D ) = M N = a 2 2 . Vậy ta chọn B.
PT
1
CM
10 tháng 8 2017
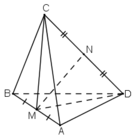
Hai tam giác CBA và DBA là hai tam giác đều cạnh a
=> ∆ CBA = ∆ DBA ( c.c.c)
=> CM = DM ( 2 đường trung tuyến tương ứng)
=> Tam giác CMD cân tại M.
Lại có: MN là đường trung tuyến nên đồng thời là đường cao: MN ⊥ CD
* Chứng minh tương tự, ta có: MN ⊥ AB
Do đó, MN là đoạn vuông góc chung của AB và CD.
* Tam giác BCD là tam giác đều cạnh a nên
SG
1
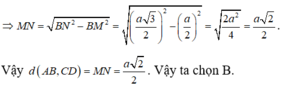
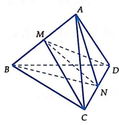
Giả thiết cho ABCD là tứ diện đều nên các cặp cạnh đối diện của tứ diện đó có vai trò như nhau. Do đó ta chỉ cần tính khoảng cách giữa hai cạnh AB và CD là đủ.
Gọi I và K lần lượt là trung điểm của AB và CD. Dễ thấy IK là đoạn vuông góc chung của AB và CD nên nó chính là khoảng cách giữa AB và CD.
Tam giác BKI vuông tại I. Ta có :