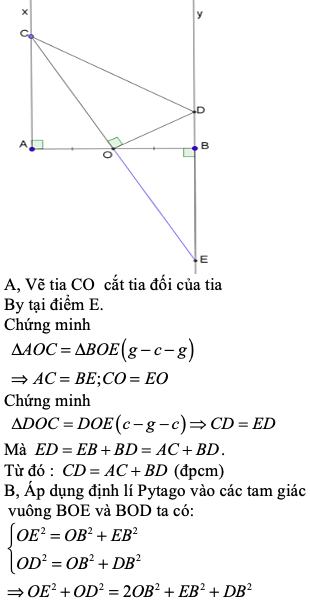
Vẽ hình chữ M ,có hai chân là tia Ax , By , điểm bụng là O ,có góc A bằng 40°, B bằng 50°, Ô bằng 90° . Chứng min Ax song song với By
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 12 2023
a: Xét ΔMHA vuông tại H và ΔMKB vuông tại K có
MA=MB
\(\widehat{MAH}=\widehat{MBK}\)(hai góc so le trong, AH//BK)
Do đó: ΔMHA=ΔMKB
=>MH=MK
b: Ta có: ΔMHA=ΔMKB
=>\(\widehat{HMA}=\widehat{KMB}\)
mà \(\widehat{KMB}+\widehat{KMA}=180^0\)(hai góc kề bù)
nên \(\widehat{HMA}+\widehat{KMA}=180^0\)
=>\(\widehat{HMK}=180^0\)
=>H,M,K thẳng hàng
18 tháng 9 2023
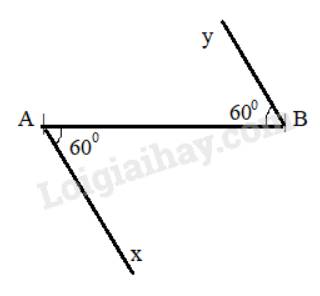
Hai đường thẳng chứa hai tia Ax và By có song song với nhau. Vì \(\widehat {xAB} = \widehat {yBA}( = 60^\circ )\), mà hai góc này ở vị trí so le trong nên Ax // By (Dấu hiệu nhận biết 2 đường thẳng song song).
CM
22 tháng 9 2017
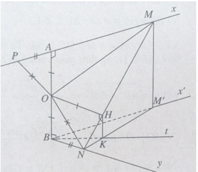
Theo giả thiết ta có M và N là hai điểm di động lần lượt trên hai tia Ax và By sao cho AM + BN = MN.
a) Kéo dài MA một đoạn AP = BN, ta có MP = MN và OP = ON.
Do đó ΔOMP = ΔOMN (c.c.c)
⇒ OA = OH nên OH = a.
Ta suy ra HM = AM và HN = BN.
b) Gọi M’ là hình chiếu vuông góc của điểm M trên mặt phẳng (Bx’, By) ta có:
HK // MM’ với K ∈ NM’.
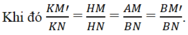
Do đó đối với tam giác BNM’ đường thẳng BK là phân giác của góc (x'By) .
c) Gọi (β) là mặt phẳng (AB, BK). Vì HK // AB nên HK nằm trong mặt phẳng (β) và do đó H thuộc mặt phẳng (β). Trong mặt phẳng (β) ta có OH = a. Vậy điểm H luôn luôn nằm trên đường tròn cố định, đường kính AB và nằm trong mặt phẳng cố định (β) = (AB, BK)
6 tháng 6 2016
Tự vẽ hình nha
a) Ta có góc xAB=ABy=80 độ
Mà 2 góc ở vị trí so le trong
Nên Ax // By
b) Ta có góc yBn+nBA=80 độ
hay 50 độ+ nBA=80 độ
=> nBa= 80-50=30 độ
Lại có góc BAm=nBA=30 độ
Mà 2 góc ở vị trí so le trong nên Am//Bn
14 tháng 8 2021
a: Xét ΔPMB và ΔPQA có
\(\widehat{PBM}=\widehat{PAQ}\)
PB=PA
\(\widehat{MPB}=\widehat{QPA}\)
Do đó: ΔPMB=ΔPQA
Suy ra: MB=AQ
Xét tứ giác AMBQ có
MB//AQ
MB=AQ
Do đó: AMBQ là hình bình hành
mà \(\widehat{MAQ}=90^0\)
nên AMBQ là hình chữ nhật
26 tháng 11 2021
Câu a có r mk ko ghi lại nx nhe
b) Ta có AQBM là HCN (CMa)
=> ^AQB=900 hay BQ ⊥ AC
=> BQ là đường cao của ΔABC
Mà H là giao điểm của 2 đường cao AI và BQ của ΔABC (gt)
=> H là trực tâm của ΔABC
=> CH cũng là đường cao của ΔABC (H là trực tâm; H ∈ CH)
=> CH ⊥ AB (đpcm)