Chứng minh tính chất a.
Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để ý rằng
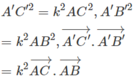
Ta có:
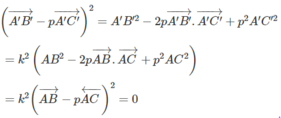
Từ đó suy ra 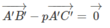
Giả sử ba điểm A, B, C thẳng hàng và điểm B nằm giữa hai điểm A và C. Khi đó A B → = t A C → , với 0 < t < 1. Áp dụng bài 1.39 ta cũng có A ' B → = t A ' C ' → , với 0 < t < 1. Do đó ba điểm A′, B′, C′ thẳng hàng và điểm B' nằm giữa hai điểm A' và C'.

a) Có 4 trường hợp một điểm nằm giữa hai điểm khác là :
- Điểm B nằm giữa A và C ;
- Điểm B nằm giữa A và D;
-Điểm C nằm giữa A và D;
-Điểm C nằm giữa B và D;
a) Có 4 trường hợp một điểm nằm giữa hai điểm khác là :
- Điểm B nằm giữa A và C ;
- Điểm B nằm giữa A và D;
-Điểm C nằm giữa A và D;
-Điểm C nằm giữa B và D;
b, Có 1 nhóm ba điểm không thẳng hàng

Ta có: a và b lần lượt là đường trung trực của các đoạn thẳng AB và BC nên \(a \bot AB,b \bot BC\).
Mà ba điểm A, B, C thẳng hàng với nhau nên đường thẳng a và b không cắt nhau và chúng cùng vuông góc với đường thẳng chứa ba điểm A, B, C.
Vậy a // b.
Phép đồng dạng tỉ số k biến 3 điểm A, B, C thẳng hàng thành 3 điểm A',B',C' sao cho:
A'B' = kAB, B'C' = kBC, A'C' = kAC
A, B, C thẳng hàng và B nằm giữa A, C ⇔ AB + BC = AC
Do đó kAB + kBC = kAC hay A'B' + B'C' = A'C'
⇒ A', B', C' thẳng hàng và B' nằm giữa A', C'