Giả sử f(x) đạt cực đại tại xo. Hãy chứng minh khẳng định 3 trong chú ý trên bằng cách xét giới hạn tỉ số f x o + ∆ x - f ' x o ∆ x khi Δx → 0 trong hai trường hợp Δx > 0 và Δx < 0.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
Hàm số f(x) xác định trên D⊆ R
Điểm
x
0
∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b)⊂ D sao cho
x
0
∈ (a;b) và f(
x
0
)>f(x),∀x ∈ (a,b)∖{
x
0
}.

Đáp án A
Hàm số f(x) xác định trên D⊆ R
Điểm xo∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b)⊂ D sao cho xo∈ (a;b) và f(xo)>f(x),∀x ∈ (a,b)∖{xo}.

Đáp án D
x 0 được gọi là điểm cực trị của hàm số y = f x nếu qua x 0 thì f ' x đổi dấu.
(I) sai vì f ' x 0 = 0 chỉ là điều kiện cần mà chưa là điều kiện đủ.
(II) sai vì hàm phân thức y = a x 2 + b x + c c x + d có cực đại, cực tiểu nhưng giá trị cực đại nhỏ hơn giá trị cực tiểu.
(III) sai vì có những hàm số chỉ có cực đại mà không có cực tiểu. Ví dụ y = − x 2 + 2 x đạt cực đại tại x=1 mà không có cực tiểu.
(IV) đúng.
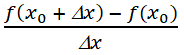 khi Δx → 0 trong hai trường hợp Δx > 0 và Δx < 0.
khi Δx → 0 trong hai trường hợp Δx > 0 và Δx < 0.


Với Δx > 0 Ta có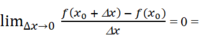 f'(xo+ ).
f'(xo+ ).
Với Δx < 0 Ta có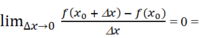 f'(xo- ).
f'(xo- ).
Vậy f’(xo) = 0.