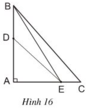
Cho hình 16. Hãy chứng minh rằng:
BE < BC;
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SG
1
19 tháng 4 2017
a) Trong hình vẽ BE < BC là hai đường xiên vẽ từ B đến đường AC và AE, AC là hai hình chiếu của chúng vì AE < AC nên BE < BC
b) EB và ED là hai đường xiên vẽ từ E đến AB
AB và AD là hai hình chiếu của chúng
Vì AD < AB nên DE < BE
Ta có: BE < BC và DE < BE nên DE < BC
PT
1
CM
24 tháng 4 2017
Trong hình vẽ D nằm giữa A và B ⇒ AD < AB
Ta có: ED, EB là hai đường xiên vẽ từ E đến đường AB
EA ⏊ AB tại A nên A là hình chiếu của E trên AB.
⇒ AD, AB lần lượt là hình chiếu của ED, EB trên AB
Trong hình vẽ D nằm giữa A và B ⇒ AD < AB nên ED < EB hay DE < BE (đường xiên nào có hình chiếu lớn hơn thì lớn hơn).
Kết hợp với kết quả câu a suy ra DE < BE < BC ⇒ DE < BC.
TB
2
PT
12 tháng 3 2017
AB \(\perp\) AC (gt)
Có E nằm giữa A và C
=> AE<AC
=> BE<BC ( qh giữa đg xiên và hình chiếu ) (1)
Có D nằm giữa A và B
=> AD<AB
=> DE<BE ( qh giữa đg xiên và hc ) (2)
Từ (1) và (2) => DE<BC
QN
12 tháng 3 2017
a) \(\widehat{BEC}\) là góc ngoài của tam giác vuông ABE nên \(\widehat{BEC}\) là góc tù.
Do đó, tam giác BEC có BE < BC (BE là cạnh đối diện với góc tù) (1)
b) Ta có: AD, AB lần lượt là hình chiếu của ED, EB lên đường thẳng AB. Vì AD < AB => ED < EB (2)
Từ (1) và (2) ta có: DE < BC
KN
24 tháng 1 2020
Theo giả thiết ta có: \(CF\perp AM\)nên \(\Delta MCF\)vuông tại F
Suy ra CF < MC (cạnh góc vuông bé hơn cạnh huyền) (1)
Tương tự ta có: BE < BM (2)
Từ (1) và (2) suy ra \(BE+CF< BM+MC=BC\)
Vậy \(BE+CF< BC\left(đpcm\right)\)
CM
1 tháng 11 2017
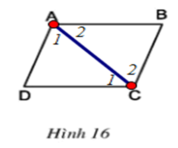
Hình thang ABCD có đáy AB, CD ⇒ AB // CD ⇒ ∠A2 = ∠C1 ̂ (hai góc so le trong)
Lại có: AD // BC ⇒ ∠A1 = ∠C2 (hai góc so le trong)
Xét ΔABC và ΔCDA có:
∠A2 = ∠C1 (cmt)
AC chung
∠A1 = ∠C2 (cmt)
⇒ ΔABC = ΔCDA (g.c.g)
⇒ AD = BC, AB = CD (các cặp cạnh tương ứng)
b)
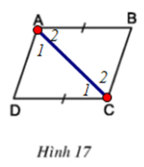
Xét ΔABC và ΔCDA có:
AC chung
∠A2 = ∠C1 (cmt)
AB = CD
⇒ ΔABC = ΔCDA (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)
∠A1 = ∠C2 (hai góc tương ứng) ⇒ AD // BC (hai góc so le trong bằng nhau)
Ta có: BE, BC là hai đường xiên vẽ từ B đến đường AC.
BA ⏊ AC tại A nên A là hình chiếu của B trên AC
⇒ AE, AC lần lượt là hình chiếu của BE, BC trên AC.
Trong hình vẽ E nằm giữa A và C ⇒ AE < AC ⇒ BE < BC (đường xiên nào có hình chiếu lớn hơn thì lớn hơn).