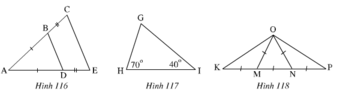
Trong các tam giác trên các hình 116, 117, 118 tam giác nào là tam giác cân tam giác nào là tam giác đều ? Vì sao?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình 118 :
Có : OM = ON = MN nên tam giác OMN đều
=> góc OMN = góc ONM
Mà : góc OMK + góc OMN = 180 độ
góc ONP + góc ONM = 180 độ
=> góc OMK = góc ONP
=> tam giác OMK = tam giác ONP ( c.g.c )
=> OK = OP ( 2 cạnh tương ứng )
=> tam giác OKP cân tại 0
Tk mk nha

Giải:
Hình 116.
Ta có: ∆ABD cân vì có AB=AD.
∆ACE cân vì AC=AE(do AB=AD,BC=DE nên AB+BC+AD+DE nên AB + BC= AD+DE hay AC= AE).
Hình 117.
Ta tính được
G= 1800-(H+I) = 1800 - (700+400)= 700
Nên ∆GHI cân vì(G=H)
Hình 118.
∆OMK là tam giác cân vì OM= MK
∆ONP là tam giác cân vì ON=OP
∆OKP là tam giác cân là vì K = P
Suy ra OKM+KOM=600
mà OKM = KOM nên =300
Tương tự OPM =300

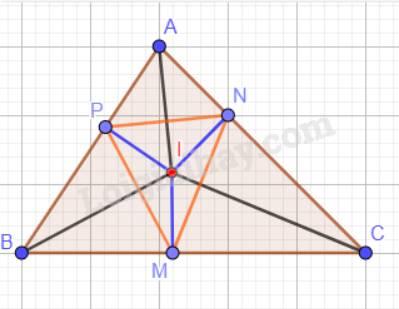
a) Trong tam giác ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác hay IM = IN = IP.
Vậy các tam giác IMN, INP, IPM có là tam giác cân tại I.
b)
Xét tam giác vuông INC và tam giác vuông IMC:
IC chung;
IN = IM.
Vậy \(\Delta INC = \Delta IMC\)(cạnh huyền – cạnh góc vuông). Suy ra: CN = CM ( 2 cạnh tương ứng).
Vậy tam giác CMN có là tam giác cân.
Tương tự, ta có: AP = AN; BP = BM.
Vậy các tam giác ANP, BPM, CMN có là tam giác cân.

Các góc trong một tam giác được gọi là góc trong. Các góc kề bù với góc trong được gọi là góc ngoài. Góc ngoài thì bằng tổng các góc trong không kề bù với nó. Mỗi tam giác chỉ có 3 góc trong và 6 góc ngoài.
Nhận xét: Góc ngoài của tam giác lớn hơn mỗi góc trong không kề với nó
- Hình 116
Ta có ΔABD cân vì AB = AD
ΔACE cân vì AC = AE
Do AB = AD , BC = DE nên AB + BC = AD + DE hay AC = AE
⇒ ΔACE cân
- Hình 117
Ta tính được
- Hình 118
* ΔOMN là tam giác đều vì ba cạnh bằng nhau OM = MN = NO
* ΔOMK cân tại M vì OM = MK
* ΔONP là tam giác cân tại N vì ON = NP