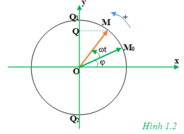
Gọi Q là hình chiếu của điểm M lên trục y (H.1.2). Chứng minh rằng điểm Q dao động điều hòa.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì cos ω t = sin( ω t + π /2) nên dao động của điểm Q trên trục y có thể viết dưới dạng y = Acos ω t. Vì vậy hiệu số pha giữa hai dao động của P và Q bằng 0.

Đáp án: B
Trong một chu kì, M đi được quãng đường bằng chu vi của đường tròn S =2πA => B sai

Đáp án C
![]()
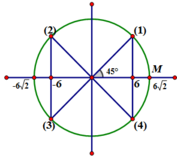
Trong 1 chu kỳ có 4 thời điểm x = 6 c m (thể hiện trên hình vẽ). Ban đầu vật đang ở M.
Có 2020 4 = 505 = 504 + 1 . Suy ra khi chuyển động 504 chu kỳ, vật đạt x = 6 c m là 2016 lần. Để đạt thêm 4 lần nữa, nó cần đi được 1 góc quét từ M đến điểm (4). Góc này bằng 315 ° ứng với 7 T 8 . Thời gian cần thiết là:
![]()

a) Xét \(\Delta EBC\)có \(\hept{\begin{cases}BE\perp AC\\DM\perp AC\end{cases}\Rightarrow}\)DM//EB => \(\frac{MC}{CE}=\frac{CD}{CB}\left(1\right)\)
Xét \(\Delta\)CFB có: \(\hept{\begin{cases}ND\perp FC\\BF\perp FC\end{cases}\Rightarrow}\)ND//BF => \(\frac{NC}{FC}=\frac{CD}{CB}\left(2\right)\)
Từ (1)(2) => \(\frac{MC}{CE}=\frac{NC}{FC}\Rightarrow MC\cdot FC=CE\cdot NC\left(đpcm\right)\)
b) Xét tam giác FBC có:\(\hept{\begin{cases}QD\perp FB\\FC\perp FB\end{cases}\Rightarrow}\)QD//FC => \(\frac{QF}{FB}=\frac{DC}{BD}\)
mà \(\frac{DC}{BD}=\frac{MC}{CE}=\frac{NC}{FC}\Rightarrow\frac{QF}{FB}=\frac{MC}{CE}=\frac{NC}{FC}\)hay \(\frac{QF}{FB}=\frac{NC}{CF}=\frac{MC}{CE}\)
=> Q,N,M thẳng hàng mà \(\frac{NC}{CF}=\frac{MC}{CE}\)=> MN//EF => QM//EF (đpcm)
c) Xét tam giác BEC có \(\hept{\begin{cases}PD\perp BE\\CE\perp BE\end{cases}}\)=> PD//EC => \(\frac{PE}{EB}=\frac{DC}{BC}\)
mà \(\frac{DC}{CB}=\frac{NK}{CF}=\frac{MC}{CE}=\frac{QF}{FB}\)
=> M,N,Q thẳng hàng (đpcm)

a: Xét tứ giác MNIH có
MH//NI
MN//IH
góc MHI=90 độ
Do đó: MNIH là hình chữ nhật
b: Xét ΔMHQ vuông tại H và ΔNIP vuông tại I có
MQ=NP
góc Q=góc P
Do đó: ΔMHQ=ΔNIP
=>QH=IP
c: Xét ΔMKQ có
MH vừa là đường cao, vừa là trung tuyến
nên ΔMKQ cân tại M
=>góc MQK=góc MKQ=góc P
=>MK//NP
mà MN//KP
nên MNPK là hình bình hành
=>MP cắt NK tại trung điểm của mỗi đường
=>M,E,P thẳng hàng
Gọi Q là hình chiếu của điểm M lên trục Oy
Ta có tọa độ y = OQ của điểm Q có phương trình là :
yQ = OMsin(ωt + φ)
Đặt OM = A, phương trình tọa độ y được viết lại là :
yQ = Asin(ωt + φ)
Vì hàm sin hay cosin là một dao động điều hòa, nên dao động của điểm Q được gọi là dao động điều hòa.