Cho AB và CD là hai đường kính vuông góc của đường tròn (O; R). Trên tia đối của tia CO lấy điểm S, SA cắt đường tròn (O) tại M. Tiếp tuyến tại M với đường tròn (O) cắt CD tại E, BM cắt CO tại F
a, Chứng minh: EM.AM = MF.OA
b, Chứng minh: ES = EM = EF
c, Gọi I là giao điểm của đoạn thẳng SB và (O). Chứng minh A, I, F thẳng hàng
d, Cho EM = R, tính FA.SM theo R
e, Kẻ MH AB. Xác định vị trí điểm M để tam giác MHO có diện tích đạt giá trị lớn nhất


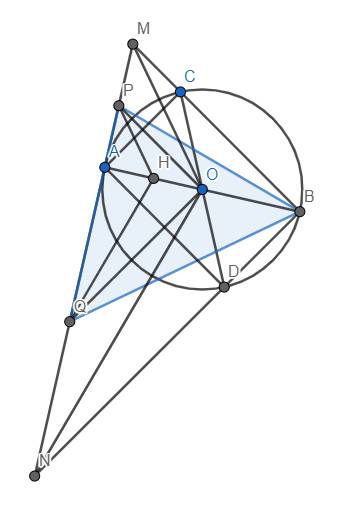
a, Chứng minh ∆MEF:∆MOA
b, ∆MEF:∆MOA mà AO=OM => ME=EF
c, Chứng minh F là trực tâm của ∆SAB, AI là đường cao, chứng minh A,I,F thẳng hàng
d, FA.SM = 2 R 2
e, S M H O = 1 2 OH.MH ≤ 1 2 . 1 2 M O 2 = 1 4 R 2
=> M ở chính giữa cung AC