Giải hệ phương trình sau: 1 + 2 x + 1 - 2 y = 5 1 + 2 x + 1 + 2 y = 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
11 tháng 8 2018
Lấy phương trình (2) trừ phương trình (1), vế trừ vế ta được:
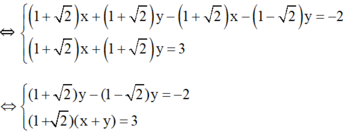
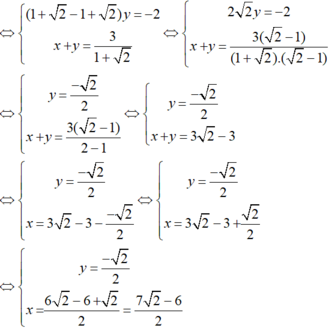
Vậy hệ phương trình có nghiệm duy nhất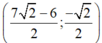 
Lưu ý:
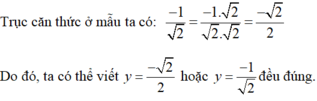
Kiến thức áp dụng
Giải hệ phương trình bằng phương pháp cộng đại số
1) Nhân hai vế của phương trình với mỗi hệ số thích hợp (nếu cần) sao cho hệ số của một trong hai ẩn bằng nhau hoặc đối nhau.
2) Áp dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn).
3) Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho và kết luận.
26 tháng 1 2022
\(\left\{{}\begin{matrix}\dfrac{x+y}{5}=\dfrac{x-y}{3}\\\dfrac{x}{4}=\dfrac{y}{2}+1\end{matrix}\right.\)<=> \(\left\{{}\begin{matrix}3x+3y=5x-5y\\x=2y+4\end{matrix}\right.\)<=> \(\left\{{}\begin{matrix}2x-8y=0\\x-2y=4\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x-4y=0\\x-2y=4\end{matrix}\right.\)<=> \(\left\{{}\begin{matrix}y=2\\x=8\end{matrix}\right.\)
AQ
1
12 tháng 10 2021
\(\left\{{}\begin{matrix}\left(x-5\right)\left(y-2\right)=\left(x+2\right)\left(y-1\right)\\\left(x-4\right)\left(y+7\right)=\left(x-3\right)\left(y+4\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy-2x-5y+10=xy-x+2y-2\\xy+7x-4y-28=xy+4x-3y-12\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+7y=12\\3x-y=16\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x+21y=36\\3x-y=16\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}22y=20\\x+7y=12\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{62}{11}\\y=\dfrac{10}{11}\end{matrix}\right.\)
HT
15 tháng 12 2016
ĐK: x khác 0
pt (2) \(\Leftrightarrow\left(x+\frac{1}{x}\right)^2+\left(y+\frac{1}{y}\right)^2=13\)
Đặt \(a=x+\frac{1}{x};b=y+\frac{1}{y}\), hệ pt trở thành:
\(\begin{cases}a+b=5\\a^2+b^2=13\end{cases}\) giải hệ pt đối xứng loại I được
\(\begin{cases}a=2\\b=3\end{cases}\) hoặc \(\begin{cases}a=3\\b=2\end{cases}\)
Thế vào được tập nghiệm của hệ pt đã cho:
\(\left\{\left(1;\frac{3-\sqrt{5}}{2}\right);\left(1;\frac{3+\sqrt{5}}{2}\right);\left(\frac{3-\sqrt{5}}{2};1\right);\left(\frac{3+\sqrt{5}}{2};1\right)\right\}\)
DV
16 tháng 12 2016
cam on minh da biet lam bai nay, truoc khi ban tra loi nen minh chua tick dung dau nhe ,mac du cach lam dung roi
6 tháng 4 2021
Bài 2:
a) Ta có: \(\Delta=\left(m-1\right)^2-4\cdot1\cdot\left(-m^2-2\right)\)
\(=m^2-2m+1+4m^2+8\)
\(=5m^2-2m+9>0\forall m\)
Do đó, phương trình luôn có hai nghiệm phân biệt với mọi m
H
6 tháng 4 2021
Bài 1:
ĐKXĐ \(2x\ne y\)
Đặt \(\dfrac{1}{2x-y}=a;x+3y=b\)
HPT trở thành
\(\left\{{}\begin{matrix}a+b=\dfrac{3}{2}\\4a-5b=-2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{3}{2}-b\\4\left(\dfrac{3}{2}-b\right)-5b=-2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{3}{2}-b\\6-9b=-2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{8}{9}\\a=\dfrac{11}{18}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+3y=\dfrac{8}{9}\\2x-y=\dfrac{18}{11}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=2x-\dfrac{18}{11}\\x+3\left(2x-\dfrac{18}{11}\right)=\dfrac{8}{9}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{82}{99}\\y=\dfrac{2}{99}\end{matrix}\right.\)
24 tháng 12 2021
\(ĐK:x,y\ne0\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{2}{y}=4\\\dfrac{2}{x}+\dfrac{3}{y}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=2\\\dfrac{1}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}+1=2\\y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\left(tm\right)\)
18 tháng 5 2021
1. \(2x^2-3x-5=0\)
\(\Leftrightarrow\left(2x-5\right)\left(x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x-5=0\\x+1=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=2,5\\x=-1\end{cases}}\)
Vậy tập ngiệm của phương trình là \(S=\left\{2,5;-1\right\}\)
18 tháng 5 2021
2x2-3x-5=0
2x2+2x-5x-5=0
2x(x+1)+5(x+1)=0
(x+1)(2x+5)=0
TH1 x+1=0 <=>x=-1
TH2 2x+5=0<=>2x=-5<=>x=-5/2
2. ta có:
2(x-2y)-(2x+y)=-1.2-8
2x-4y-2x-y=-2-8
-5y=-10
y=2
thay vào
x-2y=-1 ( với y=2)
<=> x-2.2=-1
x-4=-1
x=3
T
18 tháng 1 2021
Mình mạn phép sửa lại phương trình $2$ của bạn là $mx+3y=1$ nhé.
ĐK: $m\neq 0$
a) Khi $m=2,$ hệ phương trình là:
\(\left\{{}\begin{matrix}-4x+y=5\\2x+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4x+y=5\\4x+6y=2\end{matrix}\right.\Rightarrow7y=7\Leftrightarrow y=1\Rightarrow x=-1\)
b) \(\left\{{}\begin{matrix}-2mx+y=5\\mx+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2mx+y=5\\2mx+6y=2\end{matrix}\right.\Rightarrow7y=7\Leftrightarrow y=1\Rightarrow x=-\dfrac{2}{m}\)
c) Do ta luôn có $y=1$ là số dương nên chỉ cần chọn $m$ sao cho:
\(x=-\dfrac{2}{m}>0\Leftrightarrow m< 0\)
d) \(x^2+y^2=1\Leftrightarrow\left(-\dfrac{2}{m}\right)^2+1^2=1\Leftrightarrow\dfrac{4}{m^2}=0\) (vô lý)
Vậy không tồn tại $m$ sao cho $x^2+y^2=1.$
Lấy phương trình (2) trừ phương trình (1), vế trừ vế ta được:
Vậy hệ phương trình có nghiệm duy nhất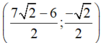
Lưu ý: