Từ một điểm A nằm bên ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với (O) trong đó B, C là các tiếp điểm. Qua điểm M thuộc cung nhỏ BC, kẻ tiếp tuyến vói (O), tiếp tuyến này cắt các tiếp tuyến AB và AC theo thứ tự ở D và E. Chứng minh chu vi tam giác ADE bằng 2AB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


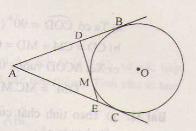
Chứng minh AB=AC; DB=DM và EC=EM.
Chu vi ΔADE bằng
= AD + DM + ME + AE
= AD + DB + EC + AE
= AB + AC
= 2AB.
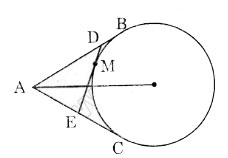
Ta có AB = AC; DB = DM;
EC = EM.
Chu vi Δ ADE:
AD +AE +DE = AD +DM + AE + EM
=AD + DB + AE + EC = AB + AC = 2AB

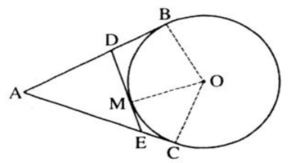
Theo tính chất hai tiếp tuyến cắt nhau ta có:
DM = DB, EM = EC, AB = AC
Chu vi ΔADE:
CΔADE = AD + DE + AE = AD + DM + ME + AE = AD + DB + EC + AE = AB + AC = 2AB (đpcm)

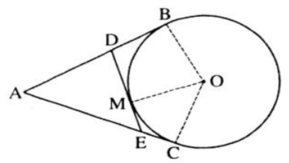
Theo tính chất hai tiếp tuyến cắt nhau ta có:
DM = DB, EM = EC, AB = AC
Chu vi ΔADE:
CΔADE = AD + DE + AE = AD + DM + ME + AE = AD + DB + EC + AE = AB + AC = 2AB (đpcm)

Ta có
DB=DM; EC=EM; AB=AC (2 tiếp tuyến cùng xp từ 1 điểm ngoài đường tròn thì khoảng cách từ điểm đó đến các tiếp điểm = nhau)
\(C_{ADE}=AD+DM+AE+EM=AD+DB+AE+EC=\)
\(=AB+AC=2AB\)

Đáp án B
* Theo tính chất hai tiếp tuyến cắt nhau ta có:
AB = AC; DB = DM; EM = EC
suy ra: DE = DM + ME = DB + EC.
* Chu vi tam giác ADE là:
AD + AE + DE = AD + AE + DB + EC
= (AD + DB ) + ( AE + EC ) = AB + AC = 2AB ( vì AB = AC )

Theo tính chất hai tiếp tuyến cắt nhau ta có:
DM = DB, EM = EC, AB = AC
Chu vi ΔADE:
CΔADE = AD + DE + AE = AD + DM + ME + AE = AD + DB + EC + AE = AB + AC = 2AB (đpcm)

a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc một đường tròn
b: Xét (O) có
DB,DM là các tiếp tuyến
Do đó: DB=DM
Xét (O) có
EM,EC là các tiếp tuyến
Do đó: EM=EC
Chu vi tam giác ADE là:
\(C_{ADE}=AD+DE+AE\)
\(=AD+DM+ME+AE\)
\(=AD+DB+CE+AE\)
\(=AB+AC=2\cdot AB\)
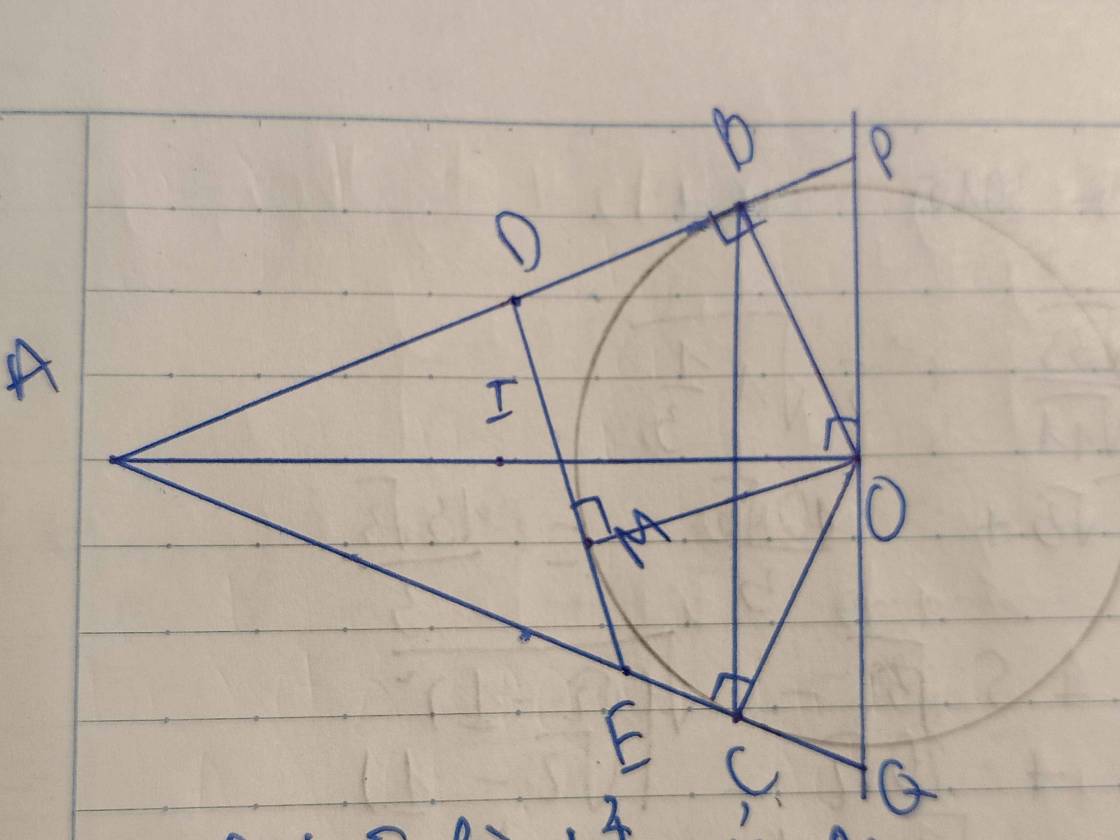
Chú ý MD = BD và ME = CE