Rút gọn 3√5a - √20a + 4√45a + √a với a ≥ 0.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 1 2017
3√5a - √20a + 4√45a + √a = 3√5a - 2√5a + 4.3√5a + √a
= 3√5a - 2√5a + 12√5a + √a = 13√5a + √a
CG
1
KH
16 tháng 10 2019
\(3\sqrt{5a}-\sqrt{20a}+4\sqrt{45a}+\sqrt{a}\)\(a\ge0\)
\(\Leftrightarrow3\sqrt{5a}-2\sqrt{5a}+12\sqrt{5a}+\sqrt{a}\)
\(\Leftrightarrow13\sqrt{5a}+\sqrt{a}\)
VẬY BIỂU THỨC ĐÃ CHO \(=13\sqrt{5a}+\sqrt{a}\)
NH
2
15 tháng 7 2019
Với a\(\ge\)0,ta có
A=\(3\sqrt{5a}-\sqrt{20a}+4\sqrt{45a}+\sqrt{a}\)
A=\(3\sqrt{5a}-\sqrt{4.5a}+4\sqrt{9.5a}+\sqrt{a}\)
A=\(3\sqrt{5a}-2\sqrt{5a}+12\sqrt{5a}+\sqrt{a}\)
A=\(13\sqrt{5a}+\sqrt{a}\)
NT
1
4 tháng 7 2017
\(3\sqrt{5a}-2\sqrt{5a}+12\sqrt{5a}+\sqrt{a}\\ =\sqrt{5a}\left(3-2+12\right)+\sqrt{a}=13\sqrt{5a}+\sqrt{a}\)
PT
1
CM
15 tháng 5 2017
Do a ≥ 0 nên bài toán luôn xác định. Ta có:
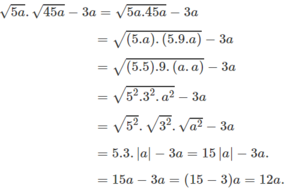
(Vì a ≥ 0 nên |a| = a)
5 tháng 8 2021
a) Ta có: \(A=\sqrt{12}+2\sqrt{27}-3\sqrt{48}\)
\(=2\sqrt{3}+6\sqrt{3}-12\sqrt{3}\)
\(=-4\sqrt{3}\)
b) Ta có: \(C=\sqrt{20a}+4\sqrt{45a}-2\sqrt{125a}\)
\(=2\sqrt{5a}+12\sqrt{5a}-10\sqrt{5a}\)
\(=4\sqrt{5a}\)
11 tháng 8 2021
a: Ta có: \(3\sqrt{5a}-\sqrt{20a}+\sqrt{45a}\)
\(=3\sqrt{5a}-2\sqrt{5a}+3\sqrt{5a}\)
\(=4\sqrt{5a}\)
b: Ta có: \(\sqrt{160a^2}+\dfrac{1}{2}\sqrt{40a^2}-3\sqrt{90a^2}\)
\(=4a\sqrt{10}+\dfrac{1}{2}\cdot2a\sqrt{10}-3\cdot3a\sqrt{10}\)
\(=-4a\sqrt{10}\)
c: Ta có: \(\sqrt{x^2-2x+1}-\sqrt{x^2-4x+4}\)
\(=\left|x-1\right|-\left|x-2\right|\)
3√5a - √20a + 4√45a + √a = 3√5a - 2√5a + 4.3√5a + √a
= 3√5a - 2√5a + 12√5a + √a = 13√5a + √a