Xét tam giác ABC vuông tại A có ∠B = α. Chứng minh rằng α = 60 o ⇔ A C A B = 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 10 2018
a)
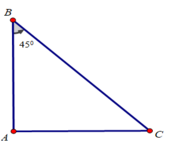
Tam giác ABC vuông tại A có ∠B = 45o ⇒ΔABC vuông cân tại A
⇒AB = AC ⇒AB/AC = 1
b)
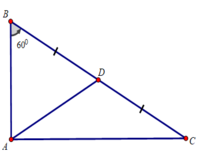
Kẻ trung tuyến AD của tam giác vuông ABC
⇒ AD = BD = BC/2
Tam giác ABD có: AD = BD, ∠(ABD) = 60o
⇒ ΔABD là tam giác đều
⇒ AB = AD = BC/2 ⇒ BC = AB
Áp dụng định lí Pytago vào tam giác ABC vuông tại A có:
AB2 + AC2 = BC2
⇔ AB2 + AC2 = 4 AB2
⇔ AC2 = 3 AB2 ⇔ AC = √3 AB
⇔ AC/AB = √3
PT
1
CM
28 tháng 11 2018
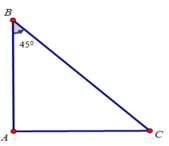
Tam giác ABC vuông tại A có ∠B = 45o ⇒ΔABC vuông cân tại A
⇒AB = AC ⇒AB/AC = 1
N
16 tháng 9 2016
ta có: B=\(\alpha\) mà \(\frac{AC}{AB}=\sqrt{3}\)→\(\tan\alpha=\sqrt{3}\)
lại có: 1+ tan2\(\alpha\)=\(\frac{1}{\cos^2\alpha}\)→cos2\(\alpha\)=\(\frac{1}{4}\)→cos \(\alpha\)=\(\frac{1}{2}\)hay \(\frac{AB}{BC}=\frac{1}{2}\)
→ C=30o(Δ vuông có 1 cạnh góc vuông = 1/2 cạnh huyền)
do đó B=600
CM
22 tháng 10 2019
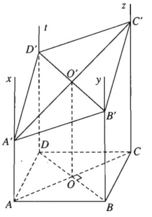
a) Ta có hai mặt phẳng song song là: (Ax, AD) // (By, BC)
Hai mặt phẳng này bị cắt bởi mặt phẳng (β) nên ta suy ra các giao tuyến của chúng phải song song nghĩa là A′D′ // B′C′.
Tương tự ta chứng minh được A′B′ // D′C′. Vậy A', B', C', D' là hình bình hành. Các hình thang AA'C'C và BB'D'D đều có OO' là đường trung bình trong đó O là tâm của hình vuông ABCD và O' là tâm của hình bình hành A',B',C',D'. Do đó: AA′ + CC′ = BB′ + DD′ = 2OO′
b) Muốn hình bình hành A',B',C',D' là hình thoi ta cần phải có A'C' ⊥ B'D'. Ta đã có AC ⊥ BD. Người ta chứng minh được rằng hình chiếu vuông góc của một góc vuông là một góc vuông khi và chỉ khi góc vuông đem chiếu có ít nhất một cạnh song song với mặt phẳng chiếu hay nằm trong mặt chiếu. Vậy A', B', C', D' là hình thoi khi và chỉ khi A'C' hoặc B'D' song song với mặt phẳng (α) cho trước. Khi đó ta có AA' = CC' hoặc BB' = DD'.
c) Muốn hình bình hành A', B', C', D' là hình chữ nhật ta cần có A'B' ⊥ B'C', nghĩa là A'B' hoặc B'C' phải song song với mặt phẳng (α)(α). Khi đó ta có AA' = BB' hoặc BB' = CC', nghĩa là hình bình hành A', B', C', D' có hai đỉnh kề nhau cách đều mặt phẳng (α) cho trước.
CM
29 tháng 12 2017
Góc 2α = A M H ^
a, Ta có: sin 2 α = A H A M = 2 A H A M = 2 A B . A C B C 2 = 2 sin α . cos α
b, 1 + cos2α = 1 + H M A M = H C A M = 2 H C B C = 2 . A C 2 B C 2 = 2 cos 2 α
c, 1 – cos2α = 1 - H M A M = H B A M = 2 H B B C = 2 . A B 2 B C 2 = 2 sin 2 α
CM
3 tháng 4 2019
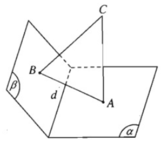
Hai mặt phẳng (α) và (β) không thể trùng nhau vì nếu chúng trùng nhau thì từ một điểm C ta dựng được hai đường thẳng CA, CB cùng vuông góc với một mặt phẳng, điều đó là vô lí.
Mặt khác (α) và (β) cũng không song song với nhau.
Vì nếu (α) // (β), thì từ CB ⊥ (β) ta suy ra CB ⊥ (α)
Như vậy từ một điểm C ta dựng được hai đường thẳng CA, CB cùng vuông góc với (α), điều đó là vô lí.
Vậy (α) và (β) là hai mặt phẳng không trùng nhau, không song song với nhau và chúng phải cắt nhau theo giao tuyến d, nghĩa là d = (α) ∩ (β)
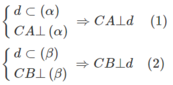
Từ (1) và (2) suy ra d ⊥ (ABC).
CM
6 tháng 2 2019
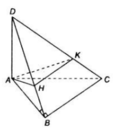
a, Ta đã chứng minh được: AE = b + c - a 2
=> AE = a + b + c - 2 a 2 = p – a
∆AIE có IE = EA.tan B A C ^ 2
= (p – a).tan B A C ^ 2
b, Chú ý: BI ⊥ FD và CI ⊥ E. Ta có:
B I C ^ = 180 0 - I B C ^ + I C D ^ = 180 0 - 1 2 A B C ^ + A C B ^
= 180 0 - 1 2 180 0 - B A C ^ = 90 0 + B A C ^ 2
Mà: E D F ^ = 180 0 - B I C ^ = 90 0 - α 2
c, BH,AI,CK cùng vuông góc với EF nên chúng song song => H B A ^ = I A B ^ (2 góc so le trong)
và K C A ^ = I A C ^ mà I A B ^ = I A C ^ nên H B A ^ = K C A ^
Vậy: ∆BHF:∆CKE
d, Do BH//DP//CK nên B D D C = H P P K mà DB = DF và CD = CE
=> H P P K = B F C E = B H C K => ∆BPH:∆CPK => B P H ^ = C P E ^
Lại có: B F P ^ = C E F ^ => ∆BPF:∆CEP (g.g)
mà B P D ^ = C P D ^ => PD là phân giác của B P C ^
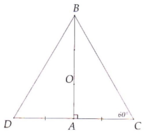
Kẻ trung tuyến AD của tam giác vuông ABC
⇒ AD = BD = BC/2
Tam giác ABD có: AD = BD, ∠(ABD) = 60o
⇒ ΔABD là tam giác đều
⇒ AB = AD = BC/2 ⇒ BC = AB
Áp dụng định lí Pytago vào tam giác ABC vuông tại A có:
AB2 + AC2 = BC2
⇔ AB2 + AC2 = 4 AB2
⇔ AC2 = 3 AB2 ⇔ AC = √3 AB
⇔ AC/AB = √3