Cho 2 cấp số cộng : 5 ;8 ;11 ; .....và 3 ;7 ;11,....Hỏi trong 100 số hạng đầu tiên của mỗi cấp số ; có bao nhiêu số hạng chung ?
A. 23
B. 24
C. 25
D. Tất cả sai
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 4 2019
Phương pháp
Cấp số cộng ( u n ) có số hạng đầu u1 và công sai d thì số hạng thứ n là
u n = u 1 + ( n - 1 ) d
Cách giải:
Gọi 198 là số hạng thứ n của dãy.
Ta có: 198 = u 1 + ( n - 1 ) d = - 2 + ( n - 1 ) . 5
⇔ 5 n = 205 ⇔ n = 41
Chọn D.
HQ
Hà Quang Minh
Giáo viên
25 tháng 8 2023
a, Số hạng tổng quát của cấp số cộng \(\left(a_n\right)\) là:
\(a_n=a_1+\left(n-1\right)d=5+\left(n-1\right)\left(-5\right)=5-5n+5=10-5n\)
b, Giả sử cấp số cộng \(\left(b_n\right)\) có công sai d, ta có:
\(b_{10}=b_1+\left(10-1\right)d\\ \Leftrightarrow20=2+9d\\ \Leftrightarrow9d=18\\ \Leftrightarrow d=2\)
Vậy số hạng tổng quát của cấp số cộng \(\left(b_n\right)\) là:
\(b_n=b_1+\left(n-1\right)d=2+\left(n-1\right)\cdot2=2+2n-2=2n\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
16 tháng 9 2023
\(Bài.1:\\ u_7=u_1+6d\\ \Leftrightarrow-10=2+6d\\ \Rightarrow6d=-10-2=-12\\ Vậy:d=\dfrac{-12}{6}=-2\\ Bài.2:S_{10}=10.u_1+\dfrac{10.\left(10-1\right)}{2}.d=10.1+\dfrac{10.9}{2}.2=100\\ Bài.3:S_{2019}=2019.u_1+\dfrac{2019.\left(2019-1\right)}{2}.d\\ =2019.3+\dfrac{2019.2018}{2}.2=2019.2021=4080399\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
16 tháng 9 2023
Bài 4:
\(d=u_2=u_1=5-2=3\)
Bài 5:
\(u_n=u_1+\left(n-1\right)d\\ \Leftrightarrow2018=2+\left(n-1\right).9\\ \Leftrightarrow2+9n-9=2018\\ \Leftrightarrow9n=2018-2+9\\ \Leftrightarrow9n=2025\\ \Leftrightarrow n=\dfrac{2025}{9}=225\)
Vậy: 2018 là số hạng thứ 225 của dãy
Bài 6:
Đề chưa có yêu cầu
CM
7 tháng 11 2018
u 1 = − 5 d = 3 → n ↔ u n = 100 100 = u n = u 1 + n − 1 d = − 5 + ( n − 1 ) .3 ⇔ 100 = 3 n − 8 ⇔ 3 n = 108 ⇔ n = 36
Chọn đáp án D
CM
12 tháng 11 2018
Phương pháp
Sử dụng tính chất của cấp số cộng
u k = u k - 1 + u k + 1 2 tìm x
Tính công sai d và sử dụng công thức tìm số hạng thứ n là
u n = u 1 + ( n - 1 ) d
Cách giải:
Áp dụng tính chất các số hạng của cấp số cộng ta có
x = - 2 + 6 2 = 2
Suy ra d = u 2 - u 1 = 4
⇒ u 5 = u 1 + 4 d = 14
Chọn D
PT
1
10 tháng 9 2023
1: u3=-3 và u9=29
=>u1+2d=-3 và u1+8d=29
=>-6d=-32 và u1+2d=-3
=>d=16/3 và u1=-3-2d=-3-32/3=-41/3
2: \(S_{20}=\dfrac{20\cdot\left[2\cdot u1+19\cdot d\right]}{2}=10\cdot\left(-5\cdot2+19\cdot3\right)\)
=10(57-10)
=10*47=470
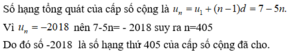
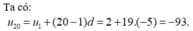
Chọn C.
Giả sử un là số hạng thứ n của cấp số cộng thứ nhất: un = 5 + 3(n – 1) và vm = 3 + (m – 1).4 là số hạng thứ m của cấp số cộng thứ 2.
un = vm khi và chỉ khi:
5 + 3(n - 1) = 3 + 4(m - 1) hay 3n + 2 = 4m - 1 ⇒ n = m/3 + m – 1
Đặt m/3 = t (t ∈ N*) ⇒ m = 3t; n= 4t - 1
Vì m; n không lớn hơn 100 nên:
Kết hợp với t là số nguyên dương nên t ∈ {1; 2; 3;…; 25}
Tương ứng với 25 giá trị của t ta được 25 số hạng chung của 2 dãy (un); (vm).