Xác định m để: Phương trình x3 – 3x2 – 9x + m = 0 có ba nghiệm phân biệt lập thành cấp số cộng.
A. m = 16
B. m = 11
C. m = 13
D. m = 12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Điều cần cần:
Giả sử phương trình có ba nghiệm phân biệt lập thành cấp số cộng.
Khi đó: x 1 + x 3 = 2 x 2 ,
Lại có :
x 1 + x 2 + x 3 = − b a = 3 ⇒ x 2 = 1
Thay vào phương trình ta được: 13 – 3.12 – 9.1 + m =0
⇔ m = 11
* Điều kiện đủ : Với m =11 phương trình trở thành :
x 3 − 3 x 2 − 9 x + 11 = 0
⇔ x − 1 x 2 − 2 x − 11 = 0 ⇔ x 1 = 1 − 12 , x 2 = 1, x 3 = 1 + 12
Ba nghiệm này lập thành cấp số cộng.
Vậy m =11 là giá trị cần tìm.

Đáp án A
Điều kiện cần: Giả sử phương trình có ba nghiệm phân biệt lập thành cấp số cộng, khi đó
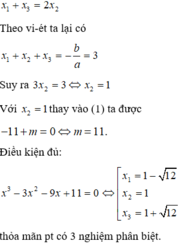

Chọn D.
Cách 1: Giải bài toán như cách giải tự luận.
- Điều kiện cần: Giả sử phương trình đã cho có ba nghiệm phân biệt x1; x2; x3 lập thành một cấp số cộng.
Theo định lý Vi-ét đối với phương trình bậc ba, ta có x1 + x2 + x3 = 3 (1)
Vì x1; x2; x3 lập thành cấp số cộng nên x1 + x3 = 2x2 (2)
Từ (1) và (2) suy ra 3x2 = 3 ⇔ x2 = 1.
Thay x2 = 1 vào phương trình đã cho, ta được
1 - 3.1 - 9.1 + m = 0 suy ra m = 11
- Điều kiện đủ:
+ Với m = 11 thì ta có phương trình x3 – 3x2 – 9x + 11 = 0 ⇔ 
Ba nghiệm này lập thành một cấp số cộng nên m = 11 là giá trị cần tìm.

Đáp án D
· Điều kiện cần:
Giả sử phương trình đã cho có 3 nghiệm phân biệt x 1 ; x 2 ; x 3 lập thành một cấp số cộng
Khi đó: x 1 + x 3 = 2 x 2 x 1 + x 2 + x 3 = 3 ⇔ 3 x 2 = 3 ⇔ x 2 = 1 .
Với x 2 = 1 thay vào phương trình ta được:
1 − 3 + m + 2 − m = 0 (luôn đúng).
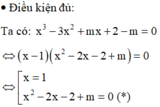
Phương trình đã cho có 3 nghiệm phân biệt tương đương với phương trình (*) có 2 nghiệm phân biệt khác 1.
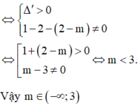

Chọn B.
Xét hàm số f(x) =
x
3
-
3
x
2
+
x
-
m
, ![]()
![]()
Điểm uốn của đồ thị hàm số là A (1;-1-m).
Phương trình x 3 - 3 x 2 + x - m = 0 có ba nghiệm phân biệt lập thành một cấp số cộng.
![]()

Chọn B
Vì ba nghiêm phân biệt x 1 , x 2 , x 3 lập thành một cấp số cộng nên ta đặt : x 1 = x 0 + d , x 2 = x 0 , x 3 = x 0 + d ( d ≠ 0 )
Theo giả thuyết Ta có: x3+3x2 – (24+m)x – 26- n= (x – x1)(x-x2)(x-x3)
=(x-xo+d)(x-xo)(x-xo-d)= x3 – 3xox2+ (3xo2-d2)x-xo3+ xod2 với mọi x

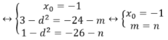
Vậy với m=n thì ba nghiệm phân biệt của phương trình lập thành một cấp số cộng

Theo hệ thức Viet: \(x_1+x_2+x_3=-\dfrac{b}{a}=3\)
Do 3 nghiệm lập thành cấp số cộng
\(\Rightarrow x_1+x_2+x_3=3x_2\)
\(\Rightarrow3x_2=3\Rightarrow x_2=1\)
Thế vào pt ban đầu:
\(\Rightarrow1-3+m+2m-1=0\Rightarrow m=1\)

Đáp án B
Giả sử phương trình đã cho có ba nghiệm phân biệt là x 1 , x 2 , x 3 theo thứ tự đó lập thành một cấp số cộng.
Suy ra 2 x 2 = x 1 + x 3 .
Lại có x − x 1 x − x 2 x − x 3 = 0 ⇔ x 3 − x 1 + x 2 + x 3 x 2 + x 1 x 2 + x 2 x 3 + x 3 x 1 x − x 1 x 2 x 3 = 0 .
Đồng nhất với phương trình x 3 + a x + b = 0 .
Suy ra x 1 + x 2 + x 3 = 0 ⇒ x 2 = 0
Thay x 2 = 0 vào phương trình đã cho ⇒ b = 0
Phương trình đã cho trở thành x 3 + a x = 0 ⇔ x = 0 x 2 + a = 0 1
Để phương trình đã cho có 3 nghiệm phân biệt thì phương trình (1) có hai nghiệm phân biệt
⇒ a < 0
Vậy b = 0, a < 0 .
Chọn B.
Giải sử phương trình có ba nghiệm phân biệt lập thành cấp số cộng.
Khi đó: x1 + x3 = 2x2, x1 + x2 + x3 = 3 ⇒ x2 = 1
Thay vào phương trình ta có m = 11.
Với m = 11 ta có phương trình : x3 – 3x2 – 9x + 11 = 0
⇔ (x – 1)(x2 – 2x – 11) = 0 ⇔
Ba nghiệm này lập thành CSC.
Vậy m = 11 là giá trị cần tìm.