Giải phương trình tan 3x. cot2x = 1
A. x = k π 2 k ∈ ℤ .
B. x = − π 4 + k π 2 k ∈ ℤ .
C. x = k π k ∈ ℤ .
D. Vô nghiệm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

-π = -3,14; -2π = -6,28; (-5π)/2 = -7,85.
Vậy (-5π)/2 < -6,32 < -2π.
Do đó điểm M nằm ở góc phần tư thứ II.
Đáp án: B

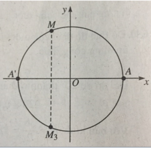
(h.66) Ta có
A M 2 = MA’ = MA + AA’
Suy ra
Sđ A M 2 = -α + π + k2π, k ∈ Z.
Vậy đáp án là B.
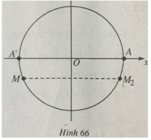
6.13. (h.67) Ta có
Sđ A M 3 = -sđ AM = -α + k2π, k ∈ Z.
Đáp án: D

Điều kiện:
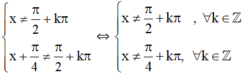
⇔ tan x.(1 - tanx) + tanx + 1 = 1 – tan x.
⇔ tan x - tan2x + 2.tan x = 0
⇔ tan2x - 3tanx = 0
⇔ tanx(tanx - 3) = 0
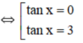
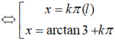
Vậy phương trình đã cho có tập nghiệm là:
{arctan 3+kπ; k ∈ Z }

\(\Leftrightarrow2x=x-\dfrac{\pi}{4}+k\pi\)
\(\Leftrightarrow x=-\dfrac{\pi}{4}+k\pi\) (\(k\in Z\))
Em nghĩ là sai. ĐKXĐ là x ≠ \(\dfrac{\pi}{4}\) + k . \(\dfrac{\pi}{2}\)
Phương trình vô nghiệm

+) Định nghĩa của sin α; cos α
Trên đường tròn lượng giác, xét cung AM có số đo α
Gọi H và K lần lượt là hình chiếu của M trên trục Ox, Oy.
Tung độ y = OK¯ của điểm M được gọi là sin của α : sin α = OK¯
Hoành độ x = OH¯ của điểm M được gọi là cos của α : cos α = OH¯
Trên đường tròn lượng giác trong mặt phẳng Oxy, lấy điểm A (1; 0) làm gốc.
Khi đó các cung có số đo hơn kém nhau một bội của 2π có điểm cuối trùng nhau.
Giả sử cung α có điểm cuối là M(x; y)
Khi đó với mọi k ∈ Z thì cung α + k2π cũng có điểm cuối là M.
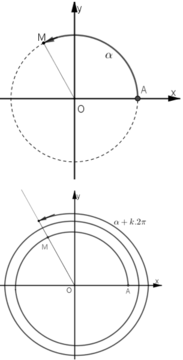
sin α = y, sin (α + k2π) = y nên sin(α + k2π) = sinα
cos α = x, cos(α + k2π) = x nên cos(α + k2π) = cosα

Đáp án D
+ Hai động động thành phần có độ lệch pha ∆ φ = ( 2 k + 1 ) π → hai dao động ngược pha => biên độ dao động tổng hợp đạt cực tiểu.
Điều kiện: cos 3 x ≠ 0 sin 2 x ≠ 0 ⇔ x ≠ π 6 + k π 3 x ≠ k π 2 k ∈ ℤ .
Phương trình tương đương:
tan 3 x = 1 cot 2 x ⇔ tan 3 x = tan 2 x ⇔ 3 x = 2 x + k π ⇔ x = k π k ∈ ℤ .
Đối chiếu điều kiện, ta thấy nghiệm x = k π không thỏa mãn x ≠ k π 2 .
Vậy phương trình đã cho vô nghiệm.
Chọn đáp án D.