Tìm nguyên hàm của hàm số:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c2 ;nhan vo duocx2(sinx/2 .cosx/2)=x2/2(sinx+cosx) lai nhan vo roi tung phan nhe

Lời giải:
Đặt \(u=\ln (x+\sqrt{x^2+1}); dv=\frac{1}{\sqrt{x^2+1}}dx\)
\(\Rightarrow du=\frac{dx}{\sqrt{x^2+1}}; v=\int \frac{x}{\sqrt{x^2+1}}dx=\frac{1}{2}\int \frac{d(x^2+1)}{\sqrt{x^2+1}}=\sqrt{x^2+1}\)
\(\Rightarrow \int \frac{x\ln (x+\sqrt{x^2+1})}{\sqrt{x^2+1}}dx=\int udv=uv-vdu=\sqrt{x^2+1}\ln (x+\sqrt{x^2+1})-\int dx\)
\(=\sqrt{x^2+1}\ln (x+\sqrt{x^2+1})-x+C\)


Lời giải:
\(\int f(x)dx=\int \frac{x^2+2x}{x+1}dx=\int \frac{(x+1)^2-1}{x+1}dx=\int (x+1-\frac{1}{x+1})dx\)
\(=\int (x+1)dx-\int \frac{1}{x+1}dx=\frac{x^2}{2}+x-\ln |x+1|+c\)

Đáp án B
Phương pháp: Sử dụng công thức ∫ 1 ( a x + b ) 2 = - 1 a ( a x + b ) + C
Cách giải: ∫ 1 ( x + 1 ) 2 d x = - 1 x + 1 + C

Chọn C
Ta có: 2 x 2 + x + 1 x - 1 = 2 x + 3 + 4 x - 1
Suy ra
I = ∫ 2 x + 3 + 4 x - 1 d x = x 2 + 3 x + 4 ln x - 1 + C
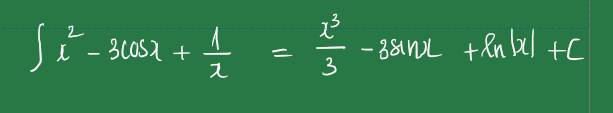
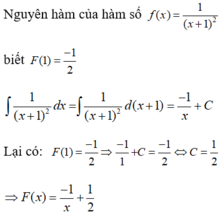
Chọn C.
Ta có:
Suy ra
I = 1 4 - 1 x - 1 + ln x + 1 x - 1 - 1 x + 1 + C