Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, S A ⊥ A B C D và S A = a 6 Tính góc giữa SC và (ABCD).
A . 30 o
B . 45 o
C . 60 o
D . 75 o
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



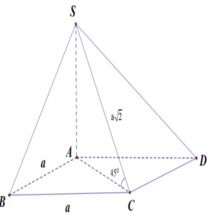
Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
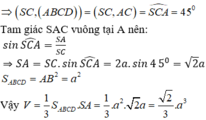

a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
SO vuông góc (ABCD)
=>(SBD) vuông góc (ABCD)
b: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
d: (SB;(ABCD))=(BS;BO)=góc SBO
cos SBO=OB/SB=a*căn 2/2/(a*căn 2)=1/2
=>góc SBO=60 độ

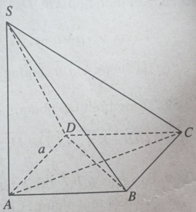
a) (BD ⊥ SA & BD ⊥ AC ⇒ BD ⊥ (SAC)
⇒ BC ⊥ SC.
b) (BC ⊥ SA & BC ⊥ AB ⇒ BC ⊥ (SAB)
⇒ (SBC) ⊥ (SAB).
c) + Xác định góc α giữa đường thẳng SC và mp(ABCD):
(C ∈(ABCD) & SA ⊥ (ABCD) ⇒ ∠[(SC,(ABCD))] = ∠(ACS) = α
+ Tính góc:
Tam tam giác vuông SCA, ta có:
tanα = SA/AC = √3/3 ⇒ α = 30 o .

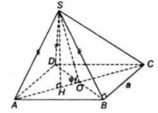
a) Tam giác ABD có AB = AD ( do ABCD là hình thoi)
=> Tam giác ABD cân tại A. Lại có góc A= 60o
=> Tam giác ABD đều.
Lại có; SA = SB = SD nên hình chóp S.ABD là hình chóp đều.
* Gọi H là tâm của tam giác ABD
=>SH ⊥ (ABD)
*Gọi O là giao điểm của AC và BD.


Hình chiếu của SC lên (ABCD) là AC.
⇒ (SC, (ABCD)) = (SC,AC) = \(\widehat{SCA}\)
Ta có: AC = a√2
Xét tam SCA vuông tại A, có: \(tan\widehat{SCA}=\dfrac{SA}{SC}=\sqrt{3}\)
\(\Rightarrow\widehat{SCA}=60^o\)

25.
\(\lim\dfrac{3.5^n+7.7^n+9}{6.5^n+9.7^n-3}=\lim\dfrac{7^n\left[3\left(\dfrac{5}{7}\right)^n+7+9.\left(\dfrac{1}{7}\right)^n\right]}{7^n\left[6\left(\dfrac{5}{7}\right)^n+9-3\left(\dfrac{1}{7}\right)^n\right]}\)
\(=\lim\dfrac{3\left(\dfrac{5}{7}\right)^n+7+9\left(\dfrac{1}{7}\right)^n}{6\left(\dfrac{5}{7}\right)^n+9-3\left(\dfrac{1}{7}\right)^n}=\dfrac{3.0+7+9.0}{6.0+9-3.0}=\dfrac{7}{9}\)
26.
\(\lim\left(n-\sqrt{n^2-4n}\right)=\lim\dfrac{\left(n-\sqrt{n^2-4n}\right)\left(n+\sqrt{n^2-4n}\right)}{n+\sqrt{n^2-4n}}\)
\(=\lim\dfrac{4n}{n+\sqrt{n^2-4n}}=\lim\dfrac{4n}{n\left(1+\sqrt{1-\dfrac{4}{n}}\right)}\)
\(=\lim\dfrac{4}{1+\sqrt{1-\dfrac{4}{n}}}=\dfrac{4}{1+\sqrt{1-0}}=2\)
26.
\(u_1=5\)
\(u_n=405=u_1.q^{n-1}\Rightarrow q^{n-1}=\dfrac{405}{5}=81\)
\(\Rightarrow q^n=81q\)
Do \(S_n=\dfrac{u_1\left(1-q^n\right)}{1-q}\Rightarrow605=\dfrac{5\left(1-81q\right)}{1-q}\)
\(\Rightarrow605-605q=5-405q\)
\(\Rightarrow q=3\)

\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=\dfrac{a\sqrt{6}}{a\sqrt{2}}=\sqrt{3}\)
\(\Rightarrow\widehat{SCA}=60^0\)


Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).