Cho hình chóp S . A B C D có đáy là hình vuông cạnh a, SA vuông góc với mặt đáy, SD tạo với mặt phẳng (SAB) một góc bằng 30 ° . Thể tích khối chóp đã cho bằng
A. 3 a 3
B. 3 a 3 3
C. 6 a 3 3
D. 6 a 3 18
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
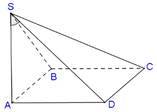
Ta có
A D ⊥ A B A D ⊥ S A ⇔ A D ⊥ S A B .
Vậy S D , S A B = S D , S A = A S D ^ = 60 0 .
Trong tam giác vuông SAD ta có
Vậy thể tích khối chóp S.ABCD bằng S A = A D . cot A S D ^ = 2 a 3 . V S A B C D = 1 3 S A B C D . S A = 1 3 4 a 2 . 2 a 3 = 8 3 a 3 9 .

Đáp án D
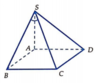
Ta có 
Vậy SB là hình chiếu vuông góc của SC lên mặt phẳng (SAB)
![]()
![]()
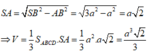

Dễ dàng chứng minh \(BC\perp BD\) (Pitago đảo) \(\Rightarrow BC\perp\left(SBD\right)\)
Đồng thời dễ dàng chứng minh \(AB\perp\left(SAD\right)\)
Từ D kẻ \(DH\perp SA\Rightarrow DH\perp\left(SAB\right)\)
Từ D kẻ \(DK\perp SB\Rightarrow DK\perp\left(SBC\right)\)
\(\Rightarrow\widehat{HDK}\) là góc giữa (SAB) và (SBC)
\(\Rightarrow\widehat{HDK}=30^0\Rightarrow DH=DK.cos30^0=\dfrac{DK\sqrt{3}}{2}\Rightarrow DH^2=\dfrac{3DK^2}{4}\)
Hệ thức lượng: \(\dfrac{1}{DH^2}=\dfrac{1}{SD^2}+\dfrac{1}{AD^2}\Leftrightarrow\dfrac{4}{3DK^2}=\dfrac{1}{SD^2}+\dfrac{1}{a^2}\Rightarrow\dfrac{1}{DK^2}=\dfrac{3}{4SD^2}+\dfrac{3}{4a^2}\) (1)
\(\dfrac{1}{DK^2}=\dfrac{1}{SD^2}+\dfrac{1}{BD^2}=\dfrac{1}{SD^2}+\dfrac{1}{2a^2}\) (2)
(1);(2) \(\Rightarrow\dfrac{3}{4SD^2}+\dfrac{3}{4a^2}=\dfrac{1}{SD^2}+\dfrac{1}{2a^2}\Rightarrow SD=a\)
\(V=\dfrac{1}{3}SD.\dfrac{1}{2}AD\left(AB+CD\right)=...\)