Cho hình lập phương A B C D . A ' B ' C ' D ' . Góc giữa hai đường thẳng AC và A'D' bằng
A. 30 °
B. 45 °
C. 60 °
D. 90 °
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow{DM}.\overrightarrow{A'N}=\left(\overrightarrow{DA}+\overrightarrow{AM}\right)\left(\overrightarrow{A'B'}+\overrightarrow{B'N}\right)\)
\(=\overrightarrow{DA}.\overrightarrow{A'B'}+\overrightarrow{AM}.\overrightarrow{A'B'}+\overrightarrow{DA}.\overrightarrow{B'N}+\overrightarrow{AM}.\overrightarrow{B'N}\)
( chứng minh được \(DA\perp A'B',AM\perp B'N\) )
\(=0+\dfrac{1}{2}\overrightarrow{AB}.\overrightarrow{AB}+\overrightarrow{C'B'}.\left(-\dfrac{1}{2}\overrightarrow{C'B'}\right)+0\)
\(=\dfrac{1}{2}AB^2-\dfrac{1}{2}C'B'^2=0\)
Suy ra \(DM\perp A'N\)
Ý A

MN là đoạn vuông góc chung \(\Rightarrow N\) là trung điểm A'D
\(\Rightarrow\dfrac{A'N}{A'D}=\dfrac{1}{2}\)

Gọi O là giao điểm của AC và BD. Dễ thấy \(\Delta OAB\) vuông tại O và \(OB=\dfrac{a\sqrt{3}}{2}\). Từ đó \(OA=\sqrt{AB^2-OB^2}=\sqrt{\left(\dfrac{\sqrt{3}}{2}a\right)^2-a^2}=\sqrt{\dfrac{1}{4}a^2}=\dfrac{a}{2}\) \(\Rightarrow AC=a\).
Vì \(SA\perp mp\left(ABCD\right)\) nên \(SA\perp AC\) tại A hay \(\Delta SAC\) vuông tại A.
Lại có \(\tan SAC=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\) nên \(\widehat{SAC}=60^o\), suy ra góc giữa SC và mp(ABCD) bằng 60o \(\Rightarrow\) Chọn A
Chỗ \(\widehat{SAC}\) em sửa lại là \(\widehat{SCA}\) mới đúng ạ.

a. Gọi cạnh lập phương là a
Ta có: \(AC=\sqrt{AB^2+AD^2}=a\sqrt{2}\)
\(AH=\sqrt{AD^2+DH^2}=a\sqrt{2}\)
\(CH=\sqrt{CD^2+DH^2}=a\sqrt{2}\)
\(\Rightarrow\Delta ACH\) đều \(\Rightarrow\widehat{CAH}=60^0\)
b.
Do \(B'C||A'D\Rightarrow\) góc giữa A'B và B'C bằng góc giữa A'B và A'D
Tương tự câu a, ta có tam giác A'BD đều \(\Rightarrow\widehat{BA'D}=60^0\)
c.
Do IJ song song SB (đường trung bình), CD song song AB \(\Rightarrow\) góc giữa IJ và CD bằng góc giữa SB và AB
Tam giác SAB đều (các cạnh bằng a) \(\Rightarrow\widehat{SBA}=60^0\)
d.
\(\overrightarrow{EG}=\overrightarrow{AC}\Rightarrow\widehat{\left(\overrightarrow{AF};\overrightarrow{EG}\right)=\widehat{\left(\overrightarrow{AF};\overrightarrow{AC}\right)}=\widehat{FAC}=60^0}\) do tam giác FAC đều
Thầy ơi thầy giúp em dạng này với ạ, em sắp thi rồi ạ :'(( https://hoc24.vn/cau-hoi/a-co-bao-nhieu-gia-tri-cua-a-de-limlimits-xrightarrowinftyleftsqrtx2-ax2021-x1righta2b-tim-a-de-ham-so-fxleftbeginmatrixdfracx31x1khixne-13akhix-1end.5243579572507

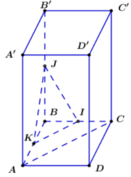
Gọi K là trung điểm của AB ⇒ IK // BC (tính chất đường trung bình của tam giác)
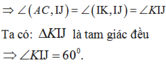
Chọn B.
Tam giác AB'C là tam giác đều nên suy ra
Chọn C.