Một mặt phẳng hoàn toàn được xác định nếu biết điều nào sau đây?
A. Ba điểm mà nó đi qua
B. Một điểm và một đường thẳng thuộc nó
C. Ba điểm không thẳng hàng
D. Hai đường thẳng thuộc mặt phẳng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Mệnh đề sai:
+ Mệnh đề (I) sai vì nếu 3 điểm đó có 2 điểm trùng nhau thì ta vẫn chưa thể xác định được mặt phẳng .
+ (II) Mặt phẳng hoàn toàn được xác định khi biết nó đi qua một điểm và chứa 1 đường thẳng không đi qua điểm đó.

a) Mặt phẳng đi qua ba điểm A, B, C đi qua đường thẳng d
b) Có một và chỉ một mặt phẳng đi qua điểm A và đường thẳng d

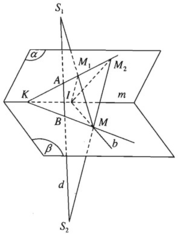
a) Mặt phẳng (M, d) cắt (α) theo giao tuyến M 1 M 2 . Điểm A cũng thuộc giao tuyến đó. Vậy đường thẳng M 1 M 2 luôn luôn đi qua điểm A cố định.
b) Mặt phẳng (M, d) cắt (β) theo giao tuyến BM. Điểm K thuộc giao tuyến đó nên ba điểm K, B, M thẳng hàng.
c) Giả sử b cắt m tại I thì mặt phẳng ( S 1 , b ) luôn luôn cắt (α) theo giao tuyến I M 1 . Do đó điểm M 1 di động trên giao tuyến của I M 1 cố định. Còn khi M di động trên b thì mặt phẳng ( S 2 , b ) cắt (α) theo giao tuyến I M 2 . Do đó điểm M 2 chạy trên giao tuyến I M 2 cố định.

B là khẳng định đúng, có vô số đường tròn đi qua 2 điểm phân biệt
Phương án A sai vì nếu ba điểm đó thẳng hàng thì chưa thể xác định được mặt phẳng.
Phương án B sai vì có vô số mặt phẳng đi qua một đường thẳng
Phương án C đúng (theo tính chất thừa nhận 2)
Phương án D sai vì hai đường thẳng có thể trùng nhau.
Chọn đáp án C.