Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
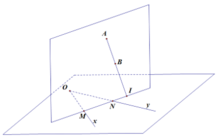
AB và mặt phẳng (Ox, Oy) luôn có điểm chung I
α chứa AB
⇒ I luôn nằm trên giao tuyến của α và (Ox, Oy) (1)
Ta lại có: α thay đổi cắt Ox tại M, Oy tại N
Xét α và (Ox, Oy) có M và N là điểm chung
⇒ MN là giao tuyến của 2 mặt phẳng (2)
(1);(2): M, N, I thẳng hàng
⇒ MN luôn đi qua I cố định

Đáp án B
Các cách xác định mặt phẳng đúng: 2; 4 ; 8
1. Đi qua 3 điểm phân biệt không thẳng hàng
3. Trong trường hợp 2 đường thẳng chéo nhau thì không thể xác định được mặt phẳng
5. Song song với 2 đường thẳng cắt nhau Có vô số mặt phẳng như vậy.
Phương pháp xác định mặt phẳng chỉ đúng khi mặt phẳng này đi qua 1 điểm cho trước
6. Song song với 2 đường thẳng chéo nhau Có vô số mặt phẳng như vậy
Phương pháp xác định mặt phẳng chỉ đúng khi mặt phẳng này đi qua 1 điểm cho trước
7. Đi qua 1 điểm và song song với một đường thẳng cho trước. Có vô số mặt phẳng như vậy

Đáp án B.
Xét các mệnh đề sau: II và III sai.
Số mệnh đề sai là 2.

Phương án A sai vì nếu ba điểm đó thẳng hàng thì chưa thể xác định được mặt phẳng.
Phương án B sai vì có vô số mặt phẳng đi qua một đường thẳng
Phương án C đúng (theo tính chất thừa nhận 2)
Phương án D sai vì hai đường thẳng có thể trùng nhau.
Chọn đáp án C.

a) Ta có: a // a’ mà a’ ⊂ (Q) nên a // (Q);
b // b’ mà b’ ⊂ (Q) nên b // (Q).
Do a // (Q);
b // (Q);
a, b cắt nhau tại M và cùng nằm trong mặt phẳng (P)
Suy ra (P) // (Q).
b) Do (R) // (Q) nên trong mp(R) tồn tại hai đường thẳng a’’, b’’ đi qua M và lần lượt song song với a’, b’ trong mp(Q).
Ta có: a // a’, a’’ // a’ nên a // a’’.
Mà a’’ ∈ (R), do đó a // (R)
Do hai mặt phẳng (P) và (R) có một điểm chung nên chúng có đường thẳng chung d.
Ta có: a // (R);
a ⊂ (P);
(P) ∩ (R) = d.
Suy ra a // d.
Mà a, d cùng nằm trong mặt phẳng (P) và cùng đi qua điểm M nên đường thẳng a chính là giao tuyến của hai mặt phẳng (P) và (R).
Chứng minh tương tự ta cũng có đường thằng b cũng là giao tuyến của hai mặt phẳng (P) và (R).
Như vậy, hai mặt phẳng (P) và (R) có hai giao tuyến a và b nên (P) và (R) là hai mặt phẳng trùng nhau.

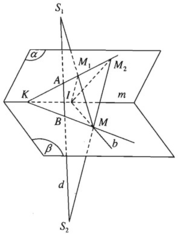
a) Mặt phẳng (M, d) cắt (α) theo giao tuyến M 1 M 2 . Điểm A cũng thuộc giao tuyến đó. Vậy đường thẳng M 1 M 2 luôn luôn đi qua điểm A cố định.
b) Mặt phẳng (M, d) cắt (β) theo giao tuyến BM. Điểm K thuộc giao tuyến đó nên ba điểm K, B, M thẳng hàng.
c) Giả sử b cắt m tại I thì mặt phẳng ( S 1 , b ) luôn luôn cắt (α) theo giao tuyến I M 1 . Do đó điểm M 1 di động trên giao tuyến của I M 1 cố định. Còn khi M di động trên b thì mặt phẳng ( S 2 , b ) cắt (α) theo giao tuyến I M 2 . Do đó điểm M 2 chạy trên giao tuyến I M 2 cố định.

Khẳng định (1) đúng vì khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại (xem mục c). Tính chất của khoảng cách giữa hai đường thẳng chéo nhau (Bài 5 – chương III).
Khẳng định (2) sai vì qua một điểm có vô số mặt phẳng vuông góc với một mặt phẳng cho trước.
Khẳng định (3) sai vì trong trường hợp đường thẳng vuông góc với mặt phẳng thì ta có vô số mặt phẳng vuông góc với mặt phẳng cho trước vì bất kì mặt phẳng nào chứa đường thẳng cũng đều vuông góc với mặt phẳng cho trước. Để có khẳng định đúng ta phải nói: Qua một đường thẳng không vuông góc với một mặt phẳng có duy nhất một mặt phẳng vuông góc với mặt phẳng đã cho.
Khẳng định (4) sai vì đường vuông góc chung của hai đường thẳng phải cắt cả hai đường ấy.
Vậy có một khẳng định đúng.
ĐÁP ÁN A

Tham khảo:
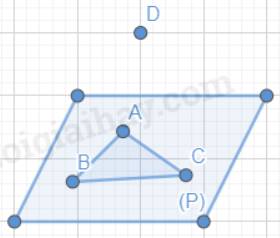
Tồn tại một và chỉ 1 mặt phẳng chứa hai đường thẳng AD và BD

Đáp án B
Mệnh đề sai:
+ Mệnh đề (I) sai vì nếu 3 điểm đó có 2 điểm trùng nhau thì ta vẫn chưa thể xác định được mặt phẳng .
+ (II) Mặt phẳng hoàn toàn được xác định khi biết nó đi qua một điểm và chứa 1 đường thẳng không đi qua điểm đó.