Chp hàm số . Tính đạo hàm của hàm số đã cho tại điểm ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`a)TXĐ: R`
`b)TXĐ: R\\{0}`
`c)TXĐ: R\\{1}`
`d)TXĐ: (-oo;-1)uu(1;+oo)`
`e)TXĐ: (-oo;-1/2)uu(1/2;+oo)`
`f)TXĐ: (-oo;-\sqrt{2})uu(\sqrt{2};+oo)`
`h)TXĐ: (-oo;0) uu(2;+oo)`
`k)TXĐ: R\\{1/2}`
`l)ĐK: {(x^2-1 > 0),(x-2 > 0),(x-1 ne 0):}`
`<=>{([(x > 1),(x < -1):}),(x > 2),(x ne 1):}`
`<=>x > 2`
`=>TXĐ: (2;+oo)`
câu l) $x^2-1 > 0$ thì giải ra 2 nghiệm $x < -1, x > 1$ mới đúng chứ nhỉ?

- TXĐ: D = R.
+ Với x = 1 ta có f ( 1 ) = k 2
+ Với x ≠ 1 ta có:
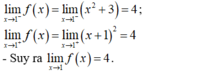
- Vậy để hàm số gián đoạn tại x = 1 khi và chỉ khi:
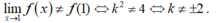
Chọn A

a) thay f(-2) vào hàm số ta có :
y=f(-2)=(-4).(-2)+3=11
thay f(-1) vào hàm số ta có :
y=f(-1)=(-4).(-1)+3=7
thay f(0) vào hàm số ta có :
y=f(0)=-4.0+3=-1
thay f(-1/2) vào hàm số ta có :
y=f(-1/2)=(-4).(-1/2)+3=5
thay f(1/2) vào hàm số ta có :
y=f(-1/2)=(-4).1/2+3=1
b)
f(x)=-1 <=> -4x+3=-1 => x=1
f(x)=-3 <=> -4x+3=-3 => x=3/2
f(x)=7 <=> -4x+3=7 => x=-1

Chọn A.
Với x = 1 ta có f(1) = k2
Với x ≠ 1 ta có
![]()
suy ra ![]() .
.
Vậy để hàm số gián đoạn tại x = 1 khi ![]() ⇔ k2 ≠ 4 ⇔ k ≠ ±2.
⇔ k2 ≠ 4 ⇔ k ≠ ±2.

Chọn B.
Xét :
![]()
Có nghiệm bội chẵn x = - 1 , x = 1 nên dấu của f’(x) qua hai nghiệm này không đổi dấu => x = 1 và x = - 1 không là cực trị
Có nghiệm bội lẻ x = 2 , x = - 3 2 , nên nó là hai cực trị
Kết luận: Hàm số có hai cực trị.
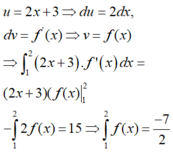
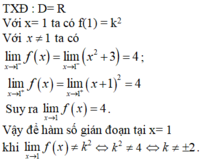
Ta có:
⇒ hàm số không liên tục tại x = 1 nên hàm số không có đạo hàm tại x0 = 1.
Chọn D.