Cho hàm số: f x = x 2 - 5 x v ớ i x > - 1 x 3 - 4 x - 1 v ớ i x < - 1
Kết luận nào sau đây không đúng?
A. Hàm số liên tục tại x= -1
B. Hàm số liên tục tại x= 1
C. Hàm số liên tục tại x= -3
D. Hàm số liên tục tại x= 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) ta có: f(2) = 2 - 3 = -1
f(5) = 5 - 3 = 2
f(-1/2) = -1/2 - 3 = -7/2
ko bít đúng ko?? 565464654654654765876546266456456456756756757
a,y = f(x) = x - 3 nếu x =3 hoặc x > 3 và = -(x - 3) nếu x < 3
b,+ Với f(2), ta có: 2 < 3
-> y = f(2) = -(2 - 3) = -(-1) = 1
+ Với f(5), ta có: 5 > 3
-> y = f(5) = 5 - 3 = 2
+ Với f(\(-\frac{1}{2}\)), ta có: \(-\frac{1}{2}\)< 3
-> y = f(\(-\frac{1}{2}\)) = -(\(-\frac{1}{2}\)- 3) = -(\(-3\frac{1}{2}\)) = \(3\frac{1}{2}\)
c, Với f(x) = \(\frac{1}{3}\), ta có:
TH1: x > 3
Ta có:y = f(x) = x - 3 = \(\frac{1}{3}\)
-> x = \(\frac{1}{3}\)+ 3 =

Chọn A
f ' ( x ) đổi dấu khi x chạy qua -1 và 3 nên hàm số có 2 điểm cực trị.

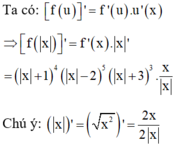
Do đó hàm số f(|x|) có 3 điểm cực trị tại x= 2; x= -2 và x= 0
Chọn B.

1) \(f\left(x\right)=2x-5\)
\(f'\left(x\right)=2\)
\(\Rightarrow f'\left(4\right)=2\)
2) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)
\(\Rightarrow y'=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)
3) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)
\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1.\left(x+9\right)}{\left(x-3\right)^2}+\dfrac{4}{2\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{12}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=2\left[\dfrac{6}{\left(x-3\right)^2}+\dfrac{1}{\sqrt[]{x}}\right]\)
\(\Rightarrow f'\left(1\right)=2\left[\dfrac{6}{\left(1-3\right)^2}+\dfrac{1}{\sqrt[]{1}}\right]=2\left(\dfrac{3}{2}+1\right)=2.\dfrac{5}{2}=5\)
Hàm số đã cho không xác định tại x=-1 nên không liên tục tại điểm đó. Tại các điểm còn lại hàm số đều liên tục. Đáp án A