Phương trình z 2 - z + 1 = 0 có hai nghiệm là
A. 1 ± 3 i 2
B. - 1 ± 3 i 2
C. 1 ± 3 i
D. - 1 ± 3 i
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(z^2-4z+5=0\Rightarrow\left\{{}\begin{matrix}z_1+z_2=4\\z_1z_2=5\end{matrix}\right.\) theo hệ thức Viet
\(w=\dfrac{z_1+z_2}{z_1z_2}+i.z_1z_2\left(z_1+z_2\right)=\dfrac{4}{5}+i.5.4=\dfrac{4}{5}+20i\)

Thay z = 1 + i vào phương trình đã cho ta có:
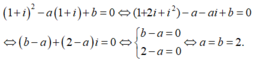
Chọn đáp án B.

Mình làm tắt nên bạn tự bổ sung nhé! (Gợi ý thôi )
a, Thay \(x=\frac{3}{2}\)vào \(\left(1\right)\left(2\right)\)thì thỏa mãn nên \(x=\frac{3}{2}\)là nghiệm chung của 2 phương trình.
b, Thay \(x=-5\)vào \(\left(2\right)\)thì thỏa mãn nên \(x=-5\)là nghiệm của \(\left(2\right)\).
Tương tự thay \(x=-5\)vào \(\left(1\right)\)thấy không thỏa mãn nên \(x=-5\)không phải nghiệm của pt \(\left(1\right)\)
c, Ta có theo câu b, \(x=-5\)là nghiệm của \(\left(2\right)\)nhưng không phải nghiệm của \(\left(1\right)\)nên pt không có cùng tập nghiệm.
\(\Rightarrow\)Hai pt trên không tương đương với nhau.
a) +) Thay \(x=\frac{3}{2}\)vào phương trình (1), ta có :
\(\Rightarrow2.\left(\frac{3}{2}\right)^2-5.\frac{3}{2}+3=0\)
\(\Leftrightarrow2.\frac{9}{4}-\frac{15}{2}+3=0\)
\(\Leftrightarrow\frac{9}{2}-\frac{15}{2}+3=0\)
\(\Leftrightarrow0=0\left(tm\right)\)
\(\Leftrightarrow x=\frac{3}{2}\)là nghiệm của phương trình (1)
+) Thay \(x=\frac{3}{2}\)vào phương trình (2), ta có :
\(\Rightarrow3-\left(\frac{2}{3}.\frac{3}{2}-1\right)\left(\frac{3}{2}+2\right)=2.\frac{3}{2}\)
\(\Leftrightarrow3-\left(1-1\right)\left(\frac{7}{2}\right)=3\)
\(\Leftrightarrow3-0=3\left(tm\right)\)
Vậy \(x=\frac{3}{2}\)là nghiệm của phương trình (2).
\(\Rightarrow\)\(x=\frac{3}{2}\)là nghiệm chung của 2 phương trình.(đpcm)
b) +) Thay \(x=-5\)vào phương trình (1), ta có :
\(\Rightarrow2.\left(-5\right)^2-5.\left(-5\right)+3=0\)
\(\Leftrightarrow2.25+25+3=0\)
\(\Leftrightarrow78=0\left(ktm\right)\)
\(\Leftrightarrow x=-5\)không là nghiệm của phương trình (1).
+) Thay \(x=-5\)vào phương trình (2), ta có :
\(\Rightarrow3-\left(\frac{2}{3}.\left(-5\right)-1\right)\left(-5+2\right)=2.\left(-5\right)\)
\(\Leftrightarrow3-\left(-\frac{10}{3}-1\right)\left(-3\right)=-10\)
\(\Leftrightarrow3-\left(-\frac{13}{3}\right)\left(-3\right)=-10\)
\(\Leftrightarrow3-13=-10\)
\(\Leftrightarrow-10=-10\left(tm\right)\)
\(\Leftrightarrow x=-5\)là nghiệm của ptr (2).
\(\Rightarrow\)Vậy x = -5 là nghiệm của phương trình (2) nhưng không là nghiệm của phương trình (1) (đpcm)
c) Hai phương trình đã cho không tương đương vì tập nghiệm của của hai phương trình không bằng nhau.

Bài 1:
ĐKXĐ: \(1\leq x\leq 3\)
Ta có:
\(\sqrt{x-1}+\sqrt{3-x}=3x^2-4x-2\)
\(\Leftrightarrow \sqrt{x-1}-1+\sqrt{3-x}-1=3x^2-4x-4\)
\(\Leftrightarrow \frac{x-2}{\sqrt{x-1}+1}+\frac{2-x}{\sqrt{3-x}+1}=(x-2)(3x+2)\)
\(\Leftrightarrow (x-2)\left(3x+2+\frac{1}{\sqrt{3-x}+1}-\frac{1}{\sqrt{x-1}+1}\right)=0(1)\)
Với mọi $1\leq x\leq 3$ ta luôn có \(3x+2\geq 5; \frac{1}{\sqrt{3-x}+1}>0; \frac{1}{\sqrt{x-1}+1}\leq 1\)
\(\Rightarrow 3x+2+\frac{1}{\sqrt{3-x}+1}-\frac{1}{\sqrt{x-1}+1}>0(2)\)
Từ (1);(2) suy ra \(x-2=0\Rightarrow x=2\)
Vậy $x=2$ là nghiệm duy nhất của pt đã cho.
Bài 2:
Với mọi $x,y,z$ nguyên không âm thì :
\(2014^z=2012^x+2013^y\geq 2012^0+2013^0=2\Rightarrow z\geq 1\)
Với $z\geq 1$ thì ta luôn có \(2012^x+2013^y=2014^z\) là số chẵn
Mà \(2013^y\) luôn lẻ nên \(2012^x\) phải lẻ. Điều này chỉ xảy ra khi $x=0$
Vậy $x=0$
Khi đó ta có: \(1+2013^y=2014^z\)
Nếu $z=1$ thì dễ thu được $y=1$
Nếu $z>1$:
Ta có: \(2014^z\vdots 4(1)\)
Mà \(2013\equiv 1\pmod 4\Rightarrow 1+2013^y\equiv 1+1\equiv 2\pmod 4\)
Tức \(1+2013^y\not\vdots 4\) (mâu thuẫn với (1))
Vậy PT có nghiệm duy nhất \((x,y,z)=(0,1,1)\)