Thu gọn đa thức ta được
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

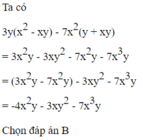

Câu 3:
a: A(x)=x^3+3x^2-4x-12
B(x)=x^3-3x^2+4x+18
A(x)+B(x)
=x^3+3x^2-4x-12+x^3-3x^2+4x+18
=2x^3+6
A(x)-B(x)
=x^3+3x^2-4x-12-x^3+3x^2-4x-18
=6x^2-8x-30
b: A(-2)=(-8)+3*4-4*(-2)-12
=-20+3*4+4*2=0
=>x=-2 là nghiệm của A(x)
B(-2)=(-8)-3*(-2)^2+4*(-2)+18=-10
=>x=-2 ko là nghiệm của B(x)

a)
\(\begin{array}{l}5{x^4} - 2{x^3}y + 20x{y^3} + 6{x^3}y - 3{x^2}{y^2} + x{y^3} - {y^4}\\ = 5{x^4} + \left( { - 2{x^3}y + 6{x^3}y} \right) - 3{x^2}{y^2} + \left( {20x{y^3} + x{y^3}} \right) - {y^4}\\ = 5{x^4} + 4{x^3}y - 3{x^2}{y^2} + 21x{y^3} - {y^4}\end{array}\)
Bậc của đa thức là: 4
b)
\(\begin{array}{l}0,6{x^3} + {x^2}z - 2,7x{y^2} + 0,4{x^3} + 1,7x{y^2}\\ = \left( {0,6{x^3} + 0,4{x^3}} \right) + {x^2}z + \left( { - 2,7x{y^2} + 1,7x{y^2}} \right)\\ = {x^3} + {x^2}z - x{y^2}\end{array}\)
Bậc của đa thức là: 3

\(C=5x^3y^2-4x^3y^2+3x^2y^3+\dfrac{1}{2}x^2y^3+\dfrac{1}{3}x^4y^5-3x^4y^5-\dfrac{1}{7}\)
\(=x^3y^2+\dfrac{7}{2}x^2y^3-\dfrac{8}{3}x^4y^5-\dfrac{1}{7}\)

Bài 2:
1: \(A=\left(x+2\right)\left(x^2-2x+4\right)+2\left(x+1\right)\left(1-x\right)\)
\(=\left(x+2\right)\left(x^2-x\cdot2+2^2\right)-2\left(x+1\right)\left(x-1\right)\)
\(=x^3+2^3-2\left(x^2-1\right)\)
\(=x^3+8-2x^2+2=x^3-2x^2+10\)
\(B=\left(2x-y\right)^2-2\left(4x^2-y^2\right)+\left(2x+y\right)^2+4\left(y+2\right)\)
\(=\left(2x-y\right)^2-2\cdot\left(2x-y\right)\left(2x+y\right)+\left(2x+y\right)^2+4\left(y+2\right)\)
\(=\left(2x-y-2x-y\right)^2+4\left(y+2\right)\)
\(=\left(-2y\right)^2+4\left(y+2\right)\)
\(=4y^2+4y+8\)
2: Khi x=2 thì \(A=2^3-2\cdot2^2+10=8-8+10=10\)
3: \(B=4y^2+4y+8\)
\(=4y^2+4y+1+7\)
\(=\left(2y+1\right)^2+7>=7>0\forall y\)
=>B luôn dương với mọi y
Bài 1:
5: \(x^2\left(x-y+1\right)+\left(x^2-1\right)\left(x+y\right)\)
\(=x^3-x^2y+x^2+x^3+x^2y-x-y\)
\(=2x^3-x+x^2-y\)
6: \(\left(3x-5\right)\left(2x+11\right)-6\left(x+7\right)^2\)
\(=6x^2+33x-10x-55-6\left(x^2+14x+49\right)\)
\(=6x^2+23x-55-6x^2-84x-294\)
=-61x-349