b) Cho y ∈ { 0; 1; 2; 3; 4; 5; 6 }. Thay y bằng chữ số thích hợp để:
chia hết cho 3
chia hết cho cả 2 và 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có \(\dfrac{a}{x}+\dfrac{b}{y}+\dfrac{c}{z}=0\Leftrightarrow ayz+bzx+cxy=0\).
Do đó: \(ax^2+by^2+cz^2=\left(ax+by+cz\right)\left(x+y+z\right)-axy-axz-byz-byx-czx-czy=0-xy\left(a+b\right)-yz\left(b+c\right)-zx\left(c+a\right)=0+xyc+yza+zxb=0\).


2: Ta có: \(\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}=\dfrac{a\left(a+b+c\right)}{b+c}+\dfrac{b\left(a+b+c\right)}{c+a}+\dfrac{c\left(a+b+c\right)}{a+b}-a-b-c=\left(a+b+c\right)\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)=a+b+c-a-b-c=0\)
1: Sửa đề: Cho \(x,y,z\ne0\) và \(\dfrac{1}{x}+\dfrac{2}{y}+\dfrac{1}{z}=\dfrac{2}{2x+y+2z}\).
CM:....
Đặt 2x = x', 2z = z'.
Ta có: \(\dfrac{2}{x'}+\dfrac{2}{y}+\dfrac{2}{z'}=\dfrac{2}{x'+y+z'}\)
\(\Leftrightarrow\dfrac{1}{x'}+\dfrac{1}{y}+\dfrac{1}{z'}=\dfrac{1}{x'+y+z'}\)
\(\Leftrightarrow\dfrac{1}{x'}-\dfrac{1}{x'+y+z'}+\dfrac{1}{y}+\dfrac{1}{z'}=0\)
\(\Leftrightarrow\dfrac{y+z'}{x'\left(x'+y+z'\right)}+\dfrac{y+z'}{yz'}=0\)
\(\Leftrightarrow\dfrac{\left(y+z'\right)\left(yz'+x'^2+x'y+x'z'\right)}{x'yz'\left(x'+y+z'\right)}=0\)
\(\Leftrightarrow\dfrac{\left(x'+y\right)\left(y+z'\right)\left(z'+x'\right)}{x'yz'\left(x'+y+z'\right)}=0\Leftrightarrow\left(2x+y\right)\left(y+2z\right)\left(2z+2x\right)=0\Leftrightarrow\left(2x+y\right)\left(y+2z\right)\left(z+x\right)=0\left(đpcm\right)\)

ta có: a+b+c=1
<=>(a+b+c)^2=1
<=>ab+bc+ca=0 (1)
mặt khác: áp dụng tính chất dãy tỉ số bằng nhau ta có:
x/a=y/b=z/c=(x+y+z)/(a+b+c)=x+y+z
<=> x=a(x+y+z) ; y=b(x+y+z) ; z=c(x+y+z)
=>xy+yz+zx=ab(x+y+z)^2+bc(x+y+z)^2+ca(x...
<=>xy+yz+zx=(ab+bc+ca)(x+y+z)^2 (2)
từ (1) và (2) ta có đpcm
Chúc bạn học giỏi!
:3

Bài 1:a) Ta có: \(1-3x⋮x-2\)
\(\Leftrightarrow-3x+1⋮x-2\)
\(\Leftrightarrow-3x+6-5⋮x-2\)
mà \(-3x+6⋮x-2\)
nên \(-5⋮x-2\)
\(\Leftrightarrow x-2\inƯ\left(-5\right)\)
\(\Leftrightarrow x-2\in\left\{1;-1;5;-5\right\}\)
hay \(x\in\left\{3;1;7;-3\right\}\)
Vậy: \(x\in\left\{3;1;7;-3\right\}\)
b) Ta có: \(3x+2⋮2x+1\)
\(\Leftrightarrow2\left(3x+2\right)⋮2x+1\)
\(\Leftrightarrow6x+4⋮2x+1\)
\(\Leftrightarrow6x+3+1⋮2x+1\)
mà \(6x+3⋮2x+1\)
nên \(1⋮2x+1\)
\(\Leftrightarrow2x+1\inƯ\left(1\right)\)
\(\Leftrightarrow2x+1\in\left\{1;-1\right\}\)
\(\Leftrightarrow2x\in\left\{0;-2\right\}\)
hay \(x\in\left\{0;-1\right\}\)
Vậy: \(x\in\left\{0;-1\right\}\)
Bài 1 :
a, Có : \(1-3x⋮x-2\)
\(\Rightarrow-3x+6-5⋮x-2\)
\(\Rightarrow-3\left(x-2\right)-5⋮x-2\)
- Thấy -3 ( x - 2 ) chia hết cho x - 2
\(\Rightarrow-5⋮x-2\)
- Để thỏa mãn yc đề bài thì : \(x-2\inƯ_{\left(-5\right)}\)
\(\Leftrightarrow x-2\in\left\{1;-1;5;-5\right\}\)
\(\Leftrightarrow x\in\left\{3;1;7;-3\right\}\)
Vậy ...
b, Có : \(3x+2⋮2x+1\)
\(\Leftrightarrow3x+1,5+0,5⋮2x+1\)
\(\Leftrightarrow1,5\left(2x+1\right)+0,5⋮2x+1\)
- Thấy 1,5 ( 2x +1 ) chia hết cho 2x+1
\(\Rightarrow1⋮2x+1\)
- Để thỏa mãn yc đề bài thì : \(2x+1\inƯ_{\left(1\right)}\)
\(\Leftrightarrow2x+1\in\left\{1;-1\right\}\)
\(\Leftrightarrow x\in\left\{0;-1\right\}\)
Vậy ...
b)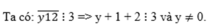
y + 3 ⋮ 3 => y ⋮ 3
Mà: y ∈ {0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6} và y ≠ 0 nên y ∈ {3 ; 6}.
Vậy số cần tìm là 312 ; 612.
Vậy số cần tìm là 120 ; 126.