chia hết cho 7 không, vì sao
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

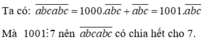

ta co 3 + 5 + 6 = 14 ma 14 chia het cho 7
nen a + b + c chia het cho 7

Các bạn trả lời giúp mình nhanh nhé, khó nhất là câu vì sao kìa. Thanks nhìu nha

Bài 2:
a) Ta có:
\(7\cdot2018\) ⇒ tích này chia hết cho 7
b) Ta có:
\(2020\cdot56\)
\(=2020\cdot8\cdot7\) ⇒ tích này chia hết cho 7
c) Ta có:
\(4\cdot23\cdot16\)
\(=2\cdot2\cdot23\cdot2\cdot2\cdot2\cdot2\) ⇒ tích này không chia hết cho 7
d) Ta có:
\(12\cdot8\cdot721\)
\(=12\cdot8\cdot103\cdot7\) ⇒ tích này chia hết cho 7

ê bạn là antifan hay ARMY thế hở, mà nếu là ARMY thì sao lại để logo thế kia, còn nếu là anti í thì sao lại có chữ ARMY dưới phần logo và nickname hở, m là gì để tao còn biết.

ta có thể viết : 5a - 9b + 2009 như sau :
5a + 5b - 14b + 2009
5 ( a + b ) - 14b + 2009
ta thấy : ( a + b ) chia hết 7 ( theo đề bài ) => 5( a + b ) chia hết 7
14b cũng chia hết 7 và 2009 cũng chia hết 7
từ đó kết luận 5a - 9b + 2009 chia hế cho 7

B = a3 + b3 + c3 - ( a + b + c )
= a3 + b3 + c3 - a - b - c
= ( a3 - a ) + ( b3 - b ) + ( c3 - c )
= a( a2 - 1 ) + b( b2 - 1 ) + c( c2 - 1 )
= ( a - 1 )a( a + 1 ) + ( b - 1 )b( b + 1 ) + ( c - 1 )c( c + 1 )
Vì ( a - 1 ) ; a ; ( a + 1 ) là ba số nguyên liên tiếp
=> sẽ có 1 số ⋮ 2 và 1 số ⋮ 3
mà (2;3) = 6 => ( a - 1 )a( a + 1 ) ⋮ 6
CMTT ta có được ( b - 1 )b( b + 1 ) ⋮ 6 và ( c - 1 )c( c + 1 ) ⋮ 6
=> ( a - 1 )a( a + 1 ) + ( b - 1 )b( b + 1 ) + ( c - 1 )c( c + 1 ) ⋮ 6
hay B = a3 + b3 + c3 - ( a + b + c ) ⋮ 6
\(B=a^3+b^3+c^3-\left(a+b+c\right)\)
\(=a^3+b^3+c^3-a-b-c\)
\(=\left(a^3-a\right)+\left(b^3-b\right)+\left(c^3-c\right)\)
\(=a\left(a^2-1\right)+b\left(b^2-1\right)+c\left(c^2-1\right)\)
\(=a\left(a-1\right)\left(a+1\right)+b\left(b-1\right)\left(b+1\right)+c\left(c-1\right)\left(c+1\right)\)
Vì \(a\), \(a-1\), \(a+1\)là 3 số nguyên liên tiếp
\(\Rightarrow a\left(a-1\right)\left(a+1\right)⋮2\)và \(a\left(a-1\right)\left(a+1\right)⋮3\)
mà \(\left(2;3\right)=1\)\(\Rightarrow a\left(a-1\right)\left(a+1\right)⋮6\)
Chứng minh tương tự: \(b\left(b-1\right)\left(b+1\right)⋮6\), \(c\left(c-1\right)\left(c+1\right)⋮6\)
\(\Rightarrow B=a\left(a-1\right)\left(a+1\right)+b\left(b-1\right)\left(b+1\right)+c\left(c-1\right)\left(c+1\right)⋮6\)
\(\Rightarrow B⋮6\)( đpcm )

Bài 3:
a chia 36 dư 12 số đó có dạng \(a=36k+12\left(k\in N\right)\)
\(\Rightarrow a=4\left(9k+3\right)\) nên a chia hết cho 4
Mà: \(9k\) ⋮ 3 ⇒ \(9k+3\) không chia hết cho 3
Nên a không chia hết cho 3
Bài 4:
a) \(x\in B\left(7\right)\) \(\Rightarrow x\in\left\{0;7;14;21;28;35;42;49;...\right\}\)
Mà: \(x\le35\)
\(\Rightarrow x\in\left\{0;7;14;21;28;35\right\}\)
b) \(x\inƯ\left(18\right)\Rightarrow x\in\left\{1;2;3;6;9;18\right\}\)
Mà: \(4< x\le10\)
\(\Rightarrow x\in\left\{6;9\right\}\)