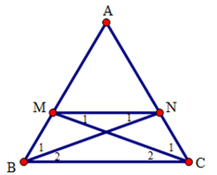
Cho tam giác ABC cân tại A. Trên cạnh AB, AC lấy các điểm M, N sao cho BM = CN. Tứ giác BMNC là hình gì? Vì sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 7 2018
\(\hept{\begin{cases}AB=AC\\BM=CN\end{cases}}\Rightarrow AN=AM\)
\(\Rightarrow\frac{AM}{AB}=\frac{A}{AC}\)
\(\Rightarrow MN//BC\text{ mà }NC=BM\)
=> MNCB là hình thang cân
4 tháng 7 2018
Ta có: \(\Delta ABC\) cân tại A => AB = AC
Mà BM = CN (gt)
=> AB - MB = AC - CN
=> AM = AN
=> M là trung điểm của AB (1)
N là trung điểm của AC (2)
Trong tam giác ABC có (1) và (2)
=> MN là đường trung bình của tam giác ABC
=> MN // BC
=> BMNC là hình thang
2 tháng 8 2021
a) Xét ΔABC có
\(\dfrac{BM}{AB}=\dfrac{CN}{AC}\left(BM=CN;AB=AC\right)\)
nên MN//BC(Định lí Ta lét đảo)
Xét tứ giác BMNC có MN//BC(cmt)
nên BMNC là hình thang
Hình thang BMNC có \(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)
nên BMNC là hình thang cân
b) \(\widehat{B}=\widehat{C}=\dfrac{180^0-40^0}{2}=70^0\)
\(\Leftrightarrow\widehat{BMN}=\widehat{MNC}=180^0-70^0=110^0\)
CM
26 tháng 5 2017
Đáp án cần chọn là: B
Ta có AB = AM + MB và AC = AN + NC
Mà AB = AC (do tam giác ABC cân tại A) và BM = NC (gt)
Suy ra AN = AM
Xét tam giác AMN cân tại A.
Suy ra A M N ^ = A N M ^ .
Xét tam giác ANM có: A ^ + A M N ^ + A N M ^ (tổng ba góc trong một tam giác)
A M N ^ = 180 0 − A 2 (vì A M N ^ = A N M ^ ) (1)
Xét tam giác ABC cân tại A ta có:
A ^ + B ^ + C ^ = 180 ° (tổng ba góc trong một tam giác) nên B ^ = 180 0 − A 2 (vì B ^ = C ^ ) (2)
Từ (1) và (2) A M N ^ = B ^
Mà B ^ , A M N ^ là hai góc đồng vị nên MN // BC
Xét tứ giác MNCB có MN // BC nên MNCB là hình thang.
Lại có B ^ = C ^ (do ΔABC cân tại A) nên MNCB là hình thang cân.
7 tháng 7 2016
a) ta có AB/AM = AC/AN (AB = AC và AM = AN theo giả thiết)
nên theo định lý đảo của định lý talet ta có MN // với BC
vậy BMNC là hình thang cân
b) xét tam giác ABC có góc A = 400. tam giác cân tại A nên ta có
góc A = góc B = (180-40):2 = 700
xét hình thang cân BMNC có:
góc BMN = góc CNM (vì đây là hai góc cùng kề 1 đáy của hình thang cân) = (360 - góc BMN - góc CNM): 2 = (360-70-70): 2 = 1100
26 tháng 8 2018
Là hình thang vì mn // bc
tg abc cân tại a => b1=c1 =[180-40]/2=70
vì bmnc là ht => b1=m=70
c1=n=70
b2 và c2 = nhau => b2=c2 =180-70=110
vậy b2=110 c2=110 n=70 m=70
8 tháng 9 2016
a)Có: AB=AM+MB
AC=AN+NC
Mà: AB=AC(gt) ; BM=CN(gt)
=>AM=AN
=> ΔAMN cân tại A
=>\(\widehat{AMN}=\frac{180-\widehat{A}}{2}\) (1)
Xét ΔABC cân tại A(gt)
=>\(\widehat{ABC}=\frac{180-\widehat{A}}{2}\) (2)
Từ (1)(2) suy ra:
^AMN=^ABC.MÀ hai góc này ở vị trí soletrong
=>MN//BC
Lại có: ^B=^C(gt)
=>BMNC là hình thang cân
b) Có: \(\widehat{MBC}=\widehat{NCB}=\frac{180-\widehat{A}}{2}=\frac{180-40}{2}=\frac{140}{2}=70\) (vì BMNC là ht)
Có: ^MBC+^BMN=180
=>^BMN=180-^MBC=180-70=110
=>^BMN=^MNC=110
∆ ABC cân tại A
⇒ ∠ B = ∠ C = ( 180 0 - ∠ A) / 2 (tính chất tam giác cân) (1)
AB = AC (gt) ⇒ AM + BM = AN + CN
Mà BM = CN (gt) ⇒ AM = AN
⇒ ∆ AMN cân tại A
⇒ ∠ M 1 = ∠ N 1 = ( 180 0 - ∠ A) / 2 (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: ∠ M 1 = ∠ B
⇒ MN // BC (vì có cặp góc đồng vị bằng nhau)
Tứ giác BCNM là hình thang có ∠ B = ∠ C
Vậy BCNM là hình thang cân.